（二）深度学习之线性回归

1. 线性回归

线性回归（linear regression）基于几个简单的假设：首先，假设自变量 $x$ 和因变量 $y$ 之间的关系是线性的，其次，假设任何噪声都比较正常，如噪声遵循正态分布。也就是说一条直线可以很好的拟合值的分布。

1.1 线性回归基础模型

通常，模型表示为：

$$\tag{1-1} \hat{y} = w^\top \cdot x + b$$

其中 $w$ 表示权重（weight），权重决定了每个特征对我们预测值的影响。 $b$ 称为偏置（bias）。偏置是指当所有特征都取值为0时，预测值应该为多少。 $x$ 表示数据特征集合。

具体如下：

$$x = \begin{bmatrix} x_1 \\ x_2 \\ : \\ x_n \end{bmatrix} ,y = \begin{bmatrix} y_1 \\ y_2 \\ : \\ y_n \end{bmatrix} ,w = \begin{bmatrix} w_1 \\ w_2 \\ : \\ w_n \end{bmatrix} ,b = \begin{bmatrix} b_1 \\ b_2 \\ : \\ b_n \end{bmatrix}$$

1.2 损失函数

在我们得到模型去拟合数据之后，我们需要确定如何评判拟合程度好坏的度量。

损失函数（loss function）能够量化目标的实际值与预测值之间的差距，提供一个评价标准。通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。

回归问题中最常用的损失函数是平方误差函数。

平方误差可以定义为下式：

$$\tag{1-2} l(w,b) = \frac{1}{2}(\hat{y}- {y})^2$$

其中样本的预测值为 $\hat{y}$，对应的真实值为 $y$。常数 $\frac{1}{2}$ 不会带来本质的差别，但是在对平方误差函数求导时可以抵消掉系数，形式上更加简单。

为了度量模型在整个数据集上的质量，我们需计算在训练集 $n$ 个样本上的损失均值。

$$\tag{1-3} L(w,b) = \frac{1}{n} \sum_{i=1}^n l(w_i,b_i) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}(w_i \cdot x_i +b_i - y_i)^2$$

得到了模型评价的方法，我们就能够在训练模型时得到更好的拟合曲线，也就是寻找到一组参数 $(w^,b^)$ 使得模型的总损失值最小。如下式：

$$\tag{1-4} (w^*,b^*) = argmin_{w,b} L(w,b)$$

1.3 梯度下降

梯度下降（gradient descent）的方法几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。

梯度下降最简单的用法是计算损失函数关于模型参数的导数（称为梯度）。 然后我们将梯度乘以一个预先确定的正数 $\alpha$ （学习率），然后让原先的参数减去这个值，得到更新过后的参数。

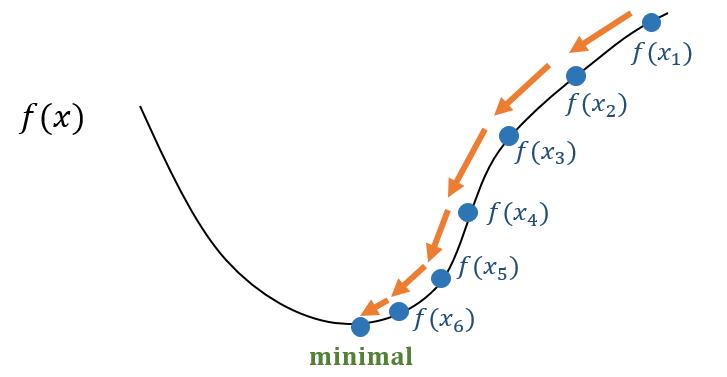
图1-1

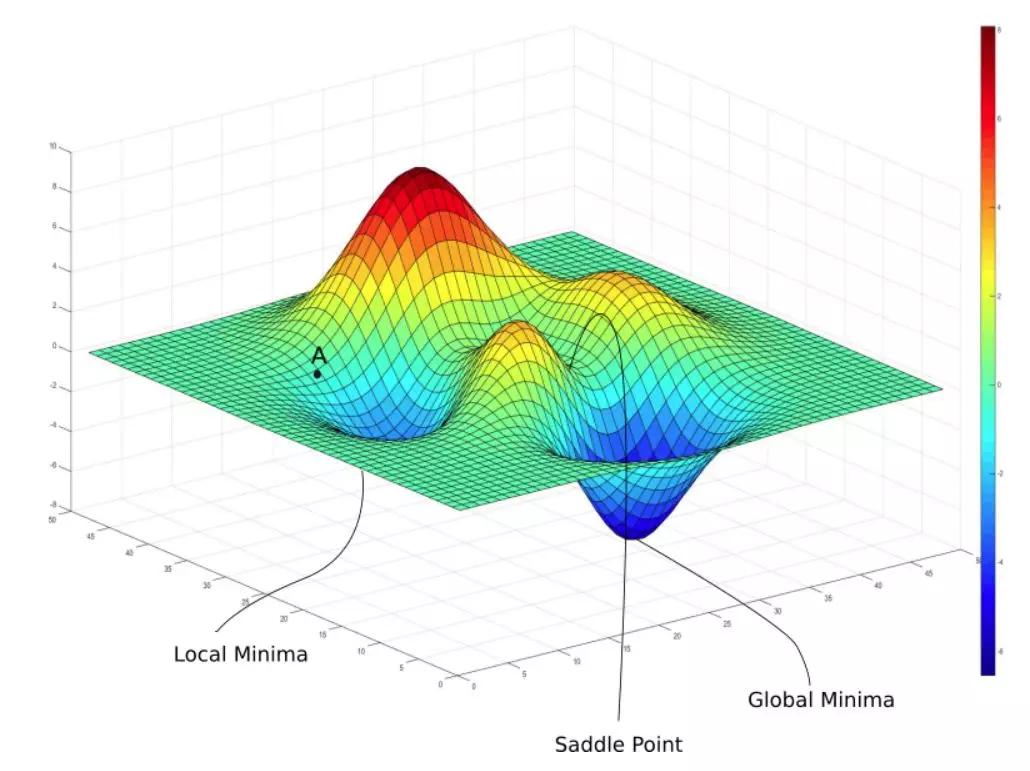
图1-2

图片来源于网络

梯度下降的一般表达式为：

$$\tag{1-5} (w,b) = (w,b) - \alpha \nabla L(w,b)$$

展开：

$$\tag{1-6} \begin{align*} w = w - \alpha \partial_w L(w,b) &= w - \frac{\alpha}{n} x \cdot (w \cdot x + b -y) \\ b = b - \alpha \partial_b L(w,b) &= b - \frac{\alpha}{n} (w \cdot x + b -y) \end{align*}$$

这些可以调整但不在训练过程中更新的参数称为超参数（hyperparameter）。调参（hyperparameter tuning）是选择超参数的过程。事实上，更难做到的是找到一组参数，这组参数能够在我们从未见过的数据上实现较低的损失，这一挑战被称为泛化（generalization）。

1.4 *小批量随机梯度下降

计算损失函数关于模型参数的梯度在实际中的执行可能会非常慢，因为在每一次更新参数之前，我们必须遍历整个数据集。因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。

$$\tag{1-7} \begin{align*} w_i &= w_i - \frac{\alpha}{|B|} \sum_{i \in B} x_i (w_i x_i + b_i -y_i) \\ b_i &= b_i - \frac{\alpha}{|B|} \sum_{i \in B}(w_i x_i + b_i -y_i) \end{align*}$$

在每次迭代中，我们首先随机抽样一个小批量 $|B|$（批量大小 batch size）， 它是由固定数量的训练样本组成的。然后，我们计算小批量的平均损失关于模型参数的梯度。最后，我们将梯度乘以一个预先确定的正数 $\alpha$，并从当前参数的值中减掉。

2. 过拟合与欠拟合问题

本篇在机器学习的篇目中会更加详细的讲解，这里就稍作解释。

进行多轮梯度下降后，可能会出现两种情况，第一种是损失函数下降的非常慢，第二种是虽然损失函数已经很小了，甚至接近零，但是不能很好的拟合下一个给出的值。这样的模型都是泛化能力差的表现。

过拟合(overfitting)和欠拟合(underfitting)是导致模型泛化能力不高的两种常见原因。

“欠拟合”常常在模型学习能力较弱，而数据复杂度较高的情况出现，此时模型由于学习能力不足，无法学习到数据集中的“一般规律”，因而导致泛化能力弱。“过拟合”常常在模型学习能力过强的情况中出现，此时的模型学习能力太强，以至于将训练集单个样本自身的特点都能捕捉到，并将其认为是“一般规律”，同样这种情况也会导致模型泛化能力下降。

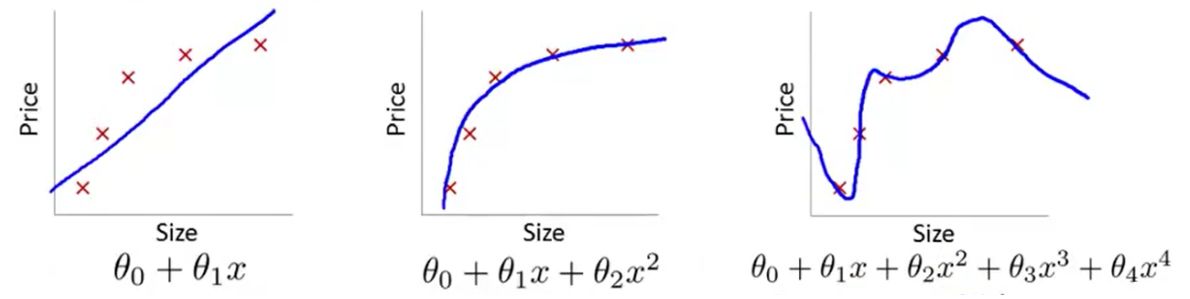
图2-1

图片来自 吴恩达机器学习

第一张图的模型过于简单，并且损失函数的收敛速度很慢。这就使得优化算法做得再好，我们的模型的泛化性能也会很差，我们把这种训练集上的偏差很大的情况叫做欠拟合。

第三张图引入了高次项，对于这样简单的问题来说这太复杂了。对于随机给出的下一个样本点，模型并不一定能很好的拟合。姑且还不谈高次模型训练过程中的开销。我们把这种和预测值和样本标签值几乎完全一致的情况叫做过拟合（Overfitting）

2.1 欠拟合解决方法

欠拟合的情况比较容易克服，常见解决方法有：

• 增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间
• 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强
• 使用非线性模型，比如核SVM 、决策树、深度学习等模型。（后续会讲到）。

2.2 过拟合解决方法

我们一般有两种方法来减小过拟合的影响：

• 减少特征值的数量，如人工筛选特征值。
• 保留所有特征值，但是减小参数θ_j的值或数量级。

其中最重要的也便是正则化。

2.3 正则化

2.3.1 L1 正则化和 L2 正则化

2.3.2 为什么正则化可以减少过拟合

2.3.3 正则化实现过程

对于深度学习来说，我们不再详细介绍优化回归模型的方法，而是选择更加复杂的非线性模型来提高模型的泛化能力。