（三）深度学习之感知机

1. 网络结构

为了更直观的表达输入数据，处理数据，输出数据这样的过程，我们习惯于使用一种网络结构图来表示。

我们可以将篇二讲到的线性回归写成一种网络结构：

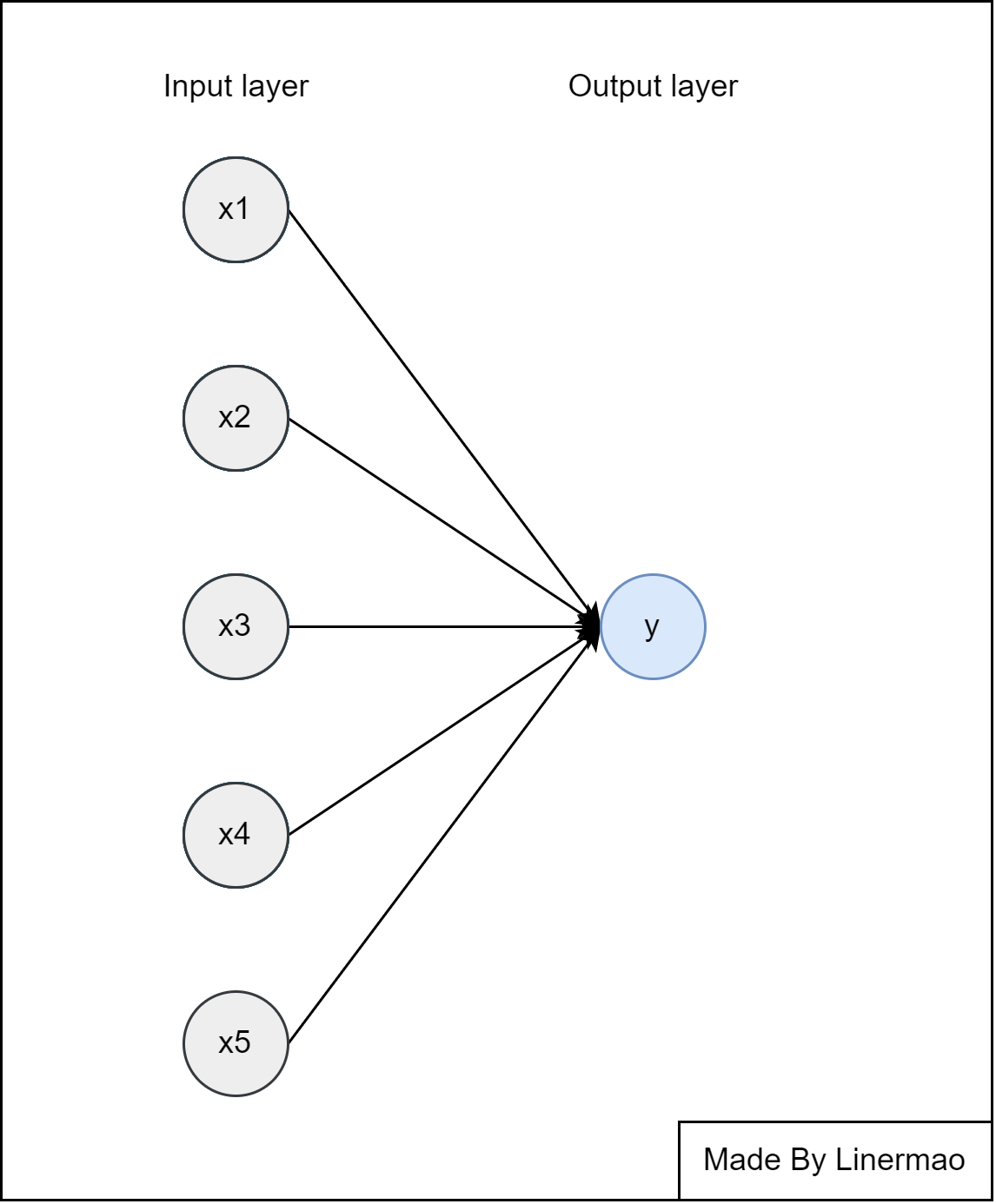
图1-1

其中，我们分为了输入层和输出层，中间连线表示 $w \cdot x +b$ 这一过程。

2. 感知机

感知机（Perceptron）是一种线性分类模型，属于判别模型。

我们定义，具有如下特征形式的式子叫做感知机：

$$\tag{2-1} f(x) = sign(w \cdot x + b)$$

$sign(x)$ 是函数符号：

$$\tag{2-2} sign(x) = \begin{cases} +1,x>0 \\ -1,x\leq0 \end{cases}$$

单个感知器可以解决二分类问题。对于具有n个元素的向量，此点将存在于n维空间中，$x$ 是一个多维向量，感知机能够找到一种分类标准来区别不同种类的特征值。

例如在纸上任意点几个点，画一条直线区分两组点，感知机能够学习到这条直线的位置，从而区分不同种类的点。

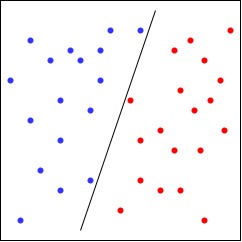
图2-1

感知机的结构与 图1-1 类似，不过此时的 $y$ 取值仅有 $1$ 或者 $-1$ 。

对于每一组 $x$ 输入，经过 $ w \cdot x + b$ 后交给 $sign(x)$ 函数判断赋值，从而实现二分类的效果。

3. Softmax 函数

如果我们更改 $sign(x)$ 函数为其他函数，就可以实现多种问题的解决。

为了能够解决更加复杂的多分类问题，我们引入了 Softmax 函数 ：

$$\tag{3-1} Softmax(x) = \frac{e^x}{\sum_{i=1}^n e^{x_i}}$$

Softmax 的含义就在于不再唯一的确定某一个最大值，而是为每个输出分类的结果都赋予一个概率值，表示属于每个类别的可能性。通过 Softmax 函数就可以将多分类的输出值转换为范围在 $[0, 1]$ 的概率分布，并且所有概率值相加得到的结果等于 $1$。

我们可以将 Softmax 应用到感知机上去，得到了可以预测多种分类结果的感知机。

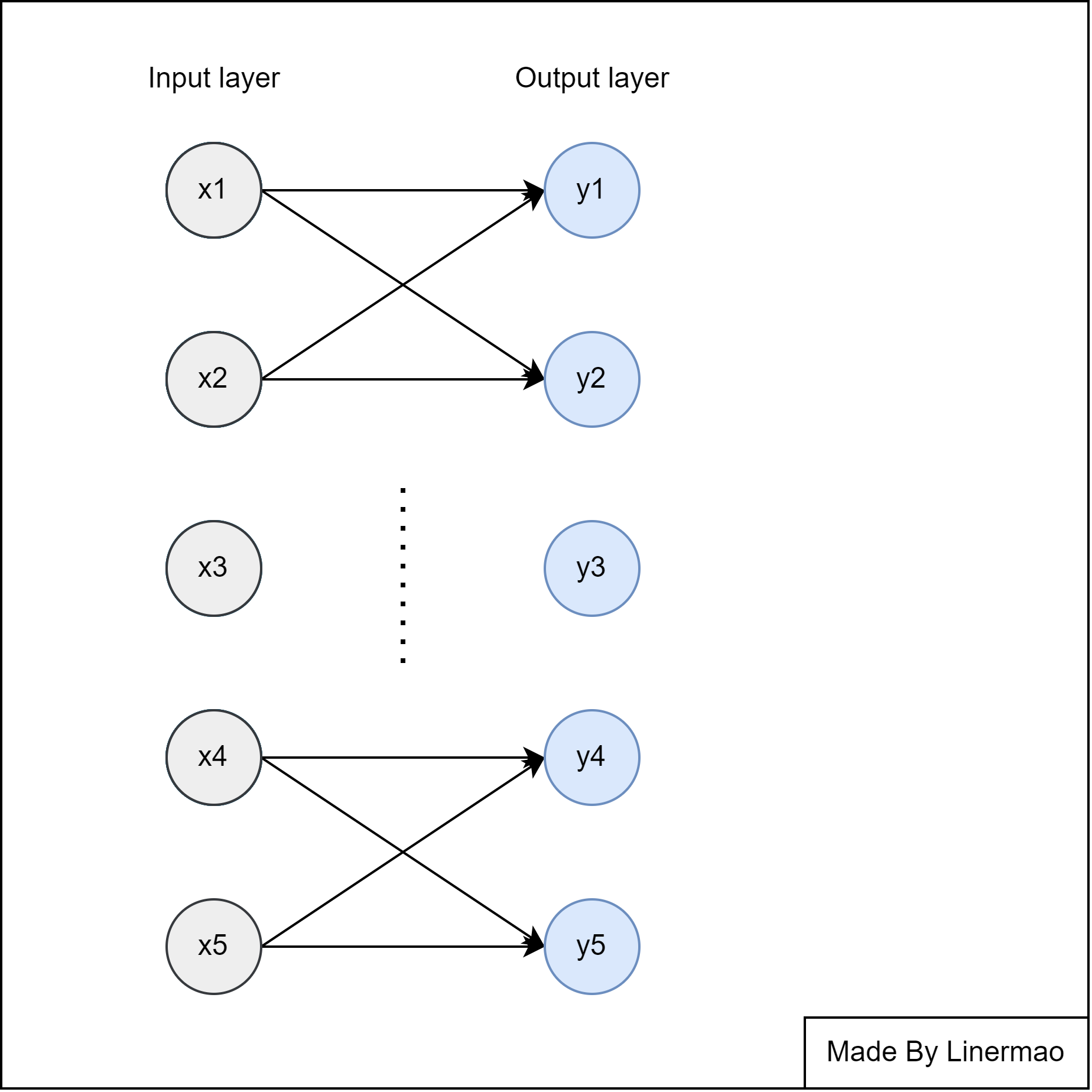
图3-1

由于我们使用了概率作为最后输出层的值，所以普通损失函数的方法已经不再适用，接下来介绍交叉熵损失函数。

4. 熵，相对熵，交叉熵

4.1 自信息

自信息（self-information）表示一个随机事件所包含的信息量。一个随机事件发生的概率越高，其自信息越低。如果一个事件必然发生，其自信息为 $0$ 。

设 $X$ 是一个有限个值的离散随机变量，概率分布为 $p(x)$，我们定义自信息为：

$$\tag{4-1} I(x) = -ln(p(x))$$

4.2 熵

香农熵（Entropy）是一个离散随机变量，其自信息的数学期望量化整个概率分布中的不确定性总量。

设 $X$ 是一个有限个值的离散随机变量，其概率分布为：

$$\tag{4-2} P(x_i \in X) = p_i, i=1,2,...,n$$

那么熵就是：

$$\tag{4-3} H(X) = -\sum_{i=1}^n p_i ln(p_i)$$

香农熵只依赖于 $X$ 的分布，而与 $X$ 的取值无关，所以香农熵也记作 $H(P)$ 。

说的简单点，香农熵代表了事件发生的不确定性，不确定性越大，香农熵越大，不确定性越小，香农熵越小。

4.3 KL散度(相对熵)

KL散度(Kullback-Leibler divergence)，也叫做 相对熵(relative entropy)。

若随机变量 $X$ 有两个单独的概率分布 $P(X)$ 和 $Q(X)$ ，可以用相对熵来衡量这两个分布的差异，相对熵的定义如下：

$$\tag{4-4} D_{KL}(P||Q) = \sum_{i=1}^n P(x_i) ln(\frac{P(x_i)}{Q(x_i)})$$

4.4 交叉熵

定义完相对熵以后，我们发现，可以使用最小化相对熵的方法使分布 $Q$ 逼近分布 $P$ 。

我们对相对熵的结构进行变形：

$$D_{KL}(P||Q) = \sum_{i=1}^n P(x_i) ln(\frac{P(x_i)}{Q (x_i)}) = \sum_{i=1}^n P(x_i) ln(P(x_i)) - \sum_{i=1}^n P(x_i) ln(Q(x_i))$$ $$\tag{4-5} D_{KL}(P||Q) = -H(P) + H(P,Q)$$

其中的 $H(P,Q)$ 就是 交叉熵 （Cross-Entropy）。

表达式就是：

$$\tag{4-6} H(P,Q) = - \sum_{i=1}^n P(x_i) ln(Q(x_i))$$

对于一个随机离散变量 $X$ 来说，他的香农熵 $H(P)$ 是一个常数，所以想要最小化相对熵，只需要通过最小化交叉熵，就可以得到分布 $P$ 的近似分布，这也是为什么可以用交叉熵作为网络的损失函数。

5. Softmax 函数和交叉熵损失函数的联合使用

当我们要进行分类时，首先需要对训练集数据进行编码，例如有猫，狗，猪三种分类，对于不同的数据的数据，我们进行下式的编码：

$$y_{cat} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , y_{dog} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} , y_{pig} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$$

我们就可以定义 $y$ 表示：

$$\tag{5-1} y = \begin{bmatrix} y_1 \\ y_2 \\ : \\ y_n \end{bmatrix} , \ y_i = \begin{cases} 1, & if \ y_i \ is \ tag \\ 0, & else \end{cases}$$

所以，带入交叉熵函数我们就可以得到交叉熵损失函数（CrossEntropyLoss）的定义，如下：

$$\tag{5-2} L(y,\hat{y}) = -y \cdot ln(\hat{y})$$

$\hat{y}$ 就是经过 Softmax 得到的输出值。

6. 多层感知机（MLP）

当遇到复杂的实际问题时，我们就会力不从心，因为感知机的本质还是一个线性预测，输入与输出之间具有一定的线性关系，而实际问题并不是可以简单拟合的，那么接下来我们就应该跳出线性的局限，进入非线性预测模型的怀抱中去。

多层感知器 (Multi-Layer Perceptron,MLP)，也叫 人工神经网络 (Artificial Neural Network,ANN)，是最简单的神经网络实现。

神经网络的名称和结构均受到人脑的启发，通过模仿生物神经元相互传递信号的方式进行学习。

图6-1

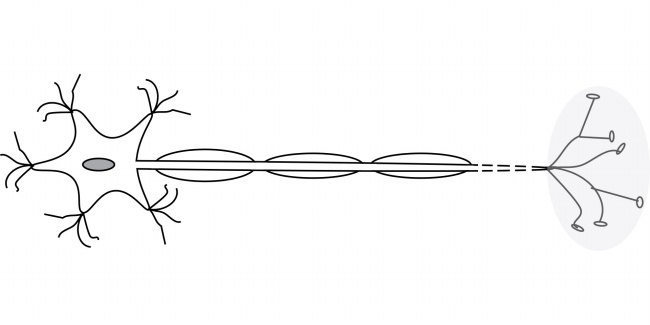
图6-2

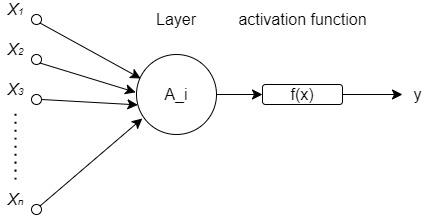
图6-3

我们通过在单个感知机网络中加入一个或多个 隐藏层 来克服线性模型的限制，使其能处理更普遍的函数关系类型。要做到这一点，最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层，直到生成最后的输出。我们可以把前 $L-1$ 层看作表示，把最后一层看作预测器。

大致的架构如下图所示：

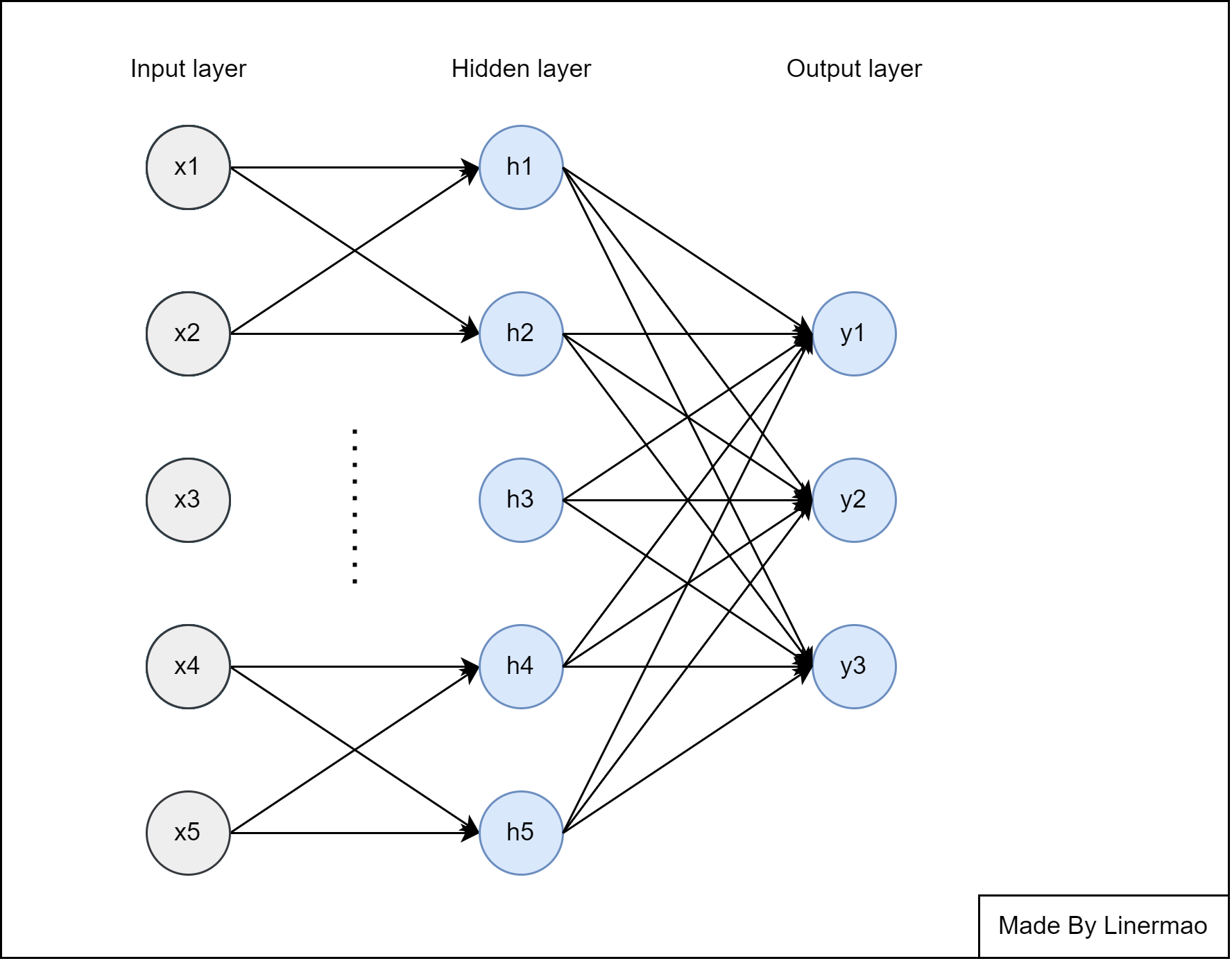
图6-4

如果仅仅是这样，增加了几个全连接的隐藏层，仍然不能实现非线性的变化，所以在隐藏层中我们增加了一个关键的要素： 激活函数 。

7. 激活函数

激活函数 (Activation Function) 是一种添加到人工神经网络中的函数，旨在帮助神经网络学习数据中复杂关系。因为神经网络中每一层的输入输出都是一个线性求和的过程，下一层的输出只是承接了上一层输入函数的线性变换，所以如果没有激活函数，那么无论你构造的神经网络多么复杂，最后的输出都是输入的线性组合，纯粹的线性组合并不能够解决更为复杂的问题。而引入非线性的激活函数之后，会给神经元引入非线性元素，使得神经网络可以逼近其他的任何非线性函数，这样可以使得神经网络应用到更多模型中。
常见的激活函数: Sigmoid激活函数，tanh(双曲正切)激活函数，ReLU激活函数 。

7.1 Sigmoid激活函数

Sigmoid函数 也叫 Logistic函数，用于隐层神经元输出，取值范围为 $(0,1)$ ，它可以将一个实数映射到 $(0,1)$ 的区间，在特征相差比较复杂或是相差不是特别大时效果比较好。

函数的表达式如下：

$$\tag{6-1} f (z) = \frac{1}{1 + e^{-z}}$$

图像类似一个S形曲线：

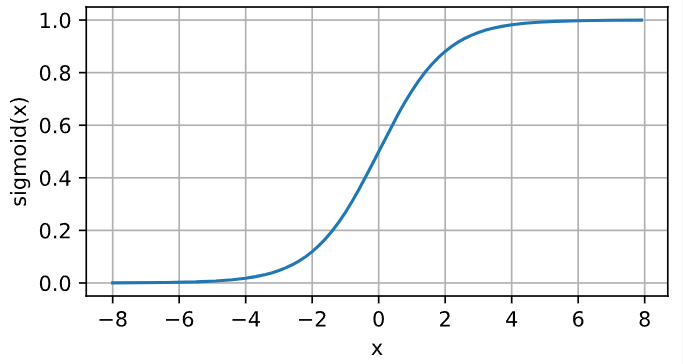
图6-5

Sigmoid函数的导数为：

$$\tag{6-2} Sigmoid'(x) = \frac{e^{-x}}{(1+e^{-x})^2} = Sigmoid(x) (1-Sigmoid(x))$$

7.2 Tanh激活函数

tanh 与 sigmoid 相比，它的输出均值为0，这使得它的收敛速度要比sigmoid快，减少了迭代更新的次数。

函数的表达式如下：

$$\tag{6-3} tanh(x) = \frac{1-e^{-2x}}{1+e^{-2x}}$$

图像如下：

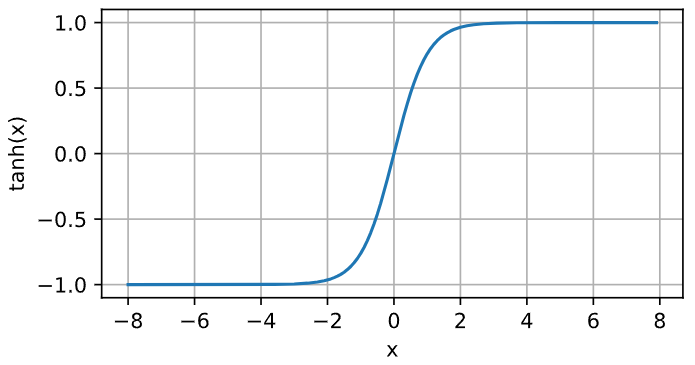
图6-6

tanh函数的导数为：

$$\tag{6-4} tanh'(x) = 1-tanh^2(x)$$

7.3 ReLU激活函数（Rectified Linear Units）

ReLU 的表达式非常简单，这使得它的计算开销相较于其他激活函数来说非常小，计算速度很快。

函数的表达式如下：

$$\tag{6-5} ReLU(x) = max(0,x)$$

图像如下：

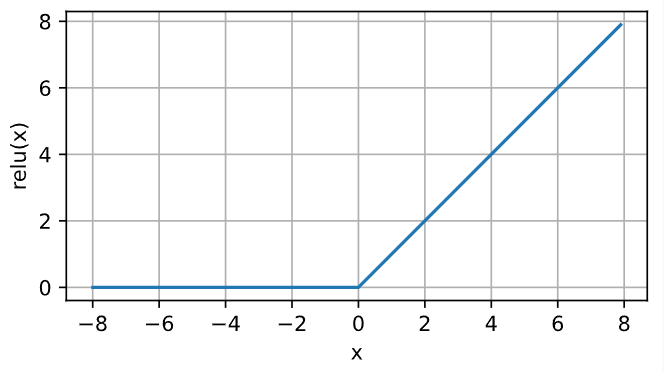
图6-7

有了激活函数以后，我们就可以用 前向传播 的方法开始训练一个非线性的网络模型了。

8. 前向传播

前向传播（Forward Propagation）是从输入层开始，经过隐藏层，计算每个隐藏层的结果并且传递到下一层直到输出层的过程。

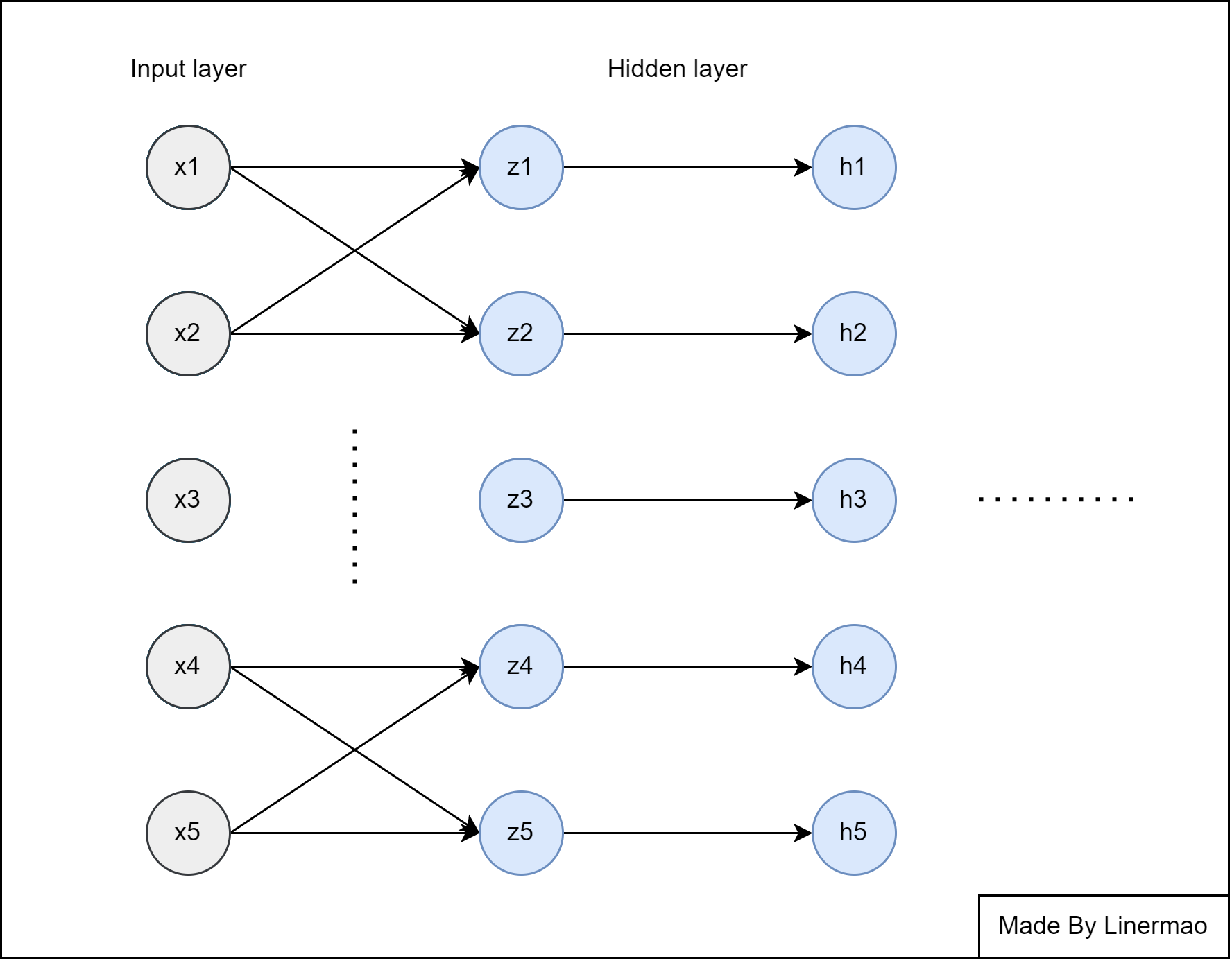
图8-1

例如 图6-1 ，我们将隐藏层分为 $z$ 层和 $h$ 层，观察隐藏层进行了什么步骤。

1. 将通过函数关系计算 $z$ 层的值:

$$\tag{8-1} z_j = \mathbf{w_j} \cdot \mathbf{x} + \mathbf{b_j},j = 1,2,...,n$$

$n$ 表示 $z$ 层神经元个数。

1. 通过激活函数来计算隐藏层 $h$ 的值:

$$\tag{8-2} \mathbf{h} = \phi(\mathbf{z})$$

1. 将此隐藏层看作下一层的输入层，重复1，2操作，直到输出层。

2. 然后根据计算所得的输出值和样本值进行比对，计算出损失项：

$$\tag{8-3} L = l(\hat{y},y)$$

1. 在篇（二）中讲到为了减少过拟合带来的问题，我们引入正则项，所以我们引入超参数 $\lambda$ ，正则化损失为：

$$\tag{8-4} J = L + s = l(\hat{y},y) + \frac{\lambda}{2} \sum_{i=1}^n \sum_{j=1}^m (w_j^{(i)})^2$$

我们将 $J$ 称为目标函数（objective function）。

可以用一张图来描述这个过程：

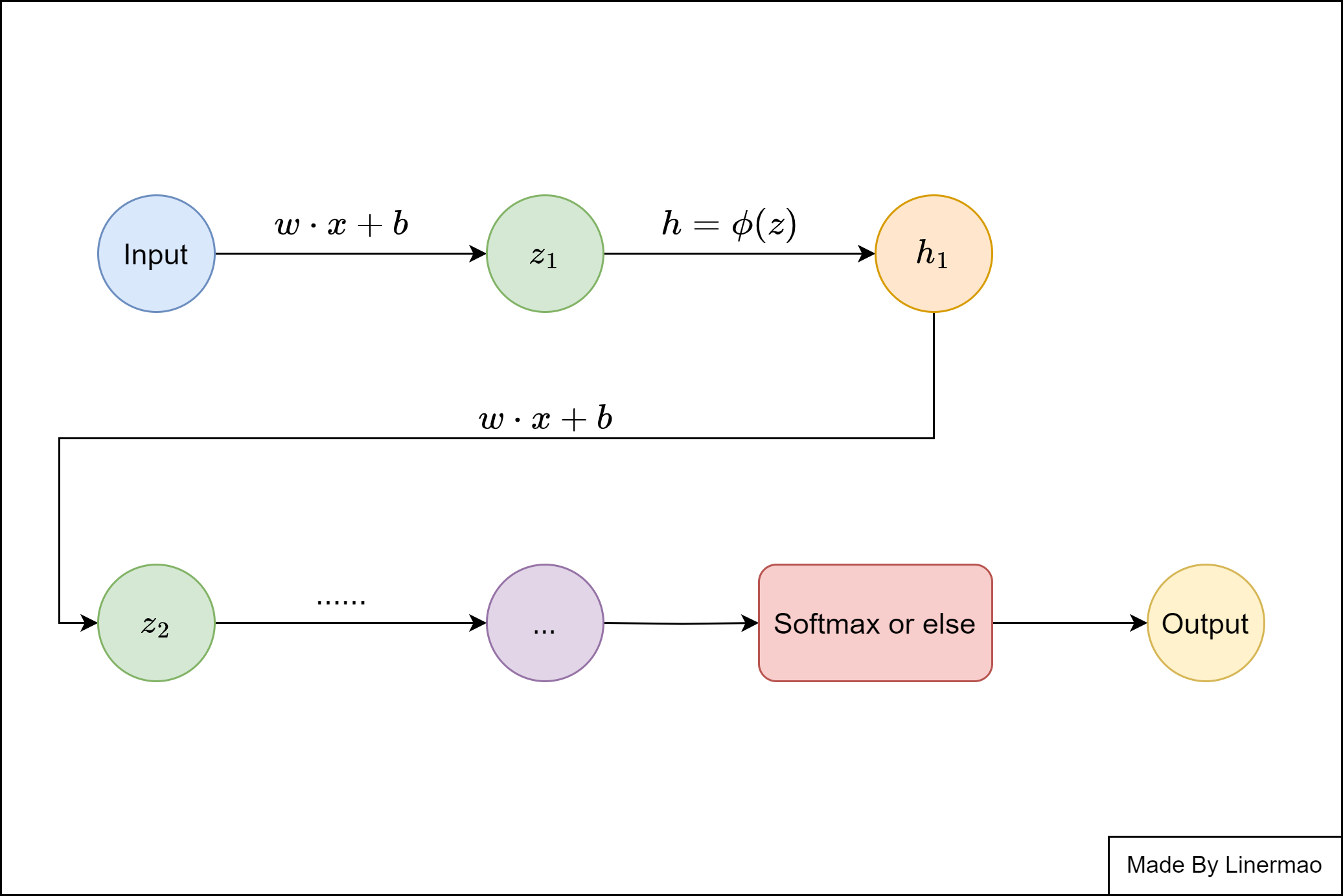
图8-2

我们显然会发现一个问题，如何去更新我们的权重和偏置呢？虽然我们得到了目标函数并致力于让其最小化，但是由于全连接网络的原因，修改一个参数会导致整个网络的结果大相径庭，并且每次修改都需要重新完成一次前向传播的过程，计算开销非常大。

下篇将会介绍反向传播的方法来帮助我们解决这个问题。