（四）深度学习之反向传播

我们使用网络结构来构建模型，使得模型能够拟合复杂的现实问题，但是也产生了权重偏置更新开销巨大的问题。下文介绍反向传播的调参思想。

1. 反向传播

反向传播（backward propagation或backpropagation）指的是计算神经网络参数梯度的方法。简言之，该方法根据微积分中的链式规则，按相反的顺序从输出层到输入层遍历网络。

1.1 链式法则

已知二元函数 $z(x,y) = f(u,v)$, $u,v$ 又分别是 $x,y$ 的函数，则 $z$ 最终是 $x,y$ 的函数： $z(x,y) = f(u(x,y),v(x,y))$

$z$ 的全微分形式是:

$$\tag{1-1} dz = \frac{\partial f}{\partial u}du + \frac{\partial f}{\partial v}dv$$

又因为$u,v$是$x,y$的函数, 可以得到$z$关于$x,y$的全微分关系:

$$\tag{1-2} dz = (\frac{\partial f}{\partial u}\frac{\partial u} {\partial x} + \frac{\partial f}{\partial v}\frac{\partial v}{\partial x}) dx + (\frac{\partial f}{\partial u}\frac {\partial u}{\partial y} + \frac{\partial f}{\partial v} \frac{\partial v}{\partial y}) dy$$

最后根据偏导数的定义就得到了：

$$\begin{align*} \tag{1-3} \frac{\partial z}{\partial x} = \frac{\partial f}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial f} {\partial v}\frac{\partial v}{\partial x} \end{align*}$$ $$\begin{align*} \tag{1-4} \frac{\partial z}{\partial y} = \frac{\partial f}{\partial u}\frac{\partial u}{\partial y} + \frac{\partial f} {\partial v}\frac{\partial v}{\partial y} \end{align*}$$

1.2 误差反向传播

要想更新权重和偏置，最简单的方法就是 梯度下降法 （见篇（二）），也就是说，我们只需要求得 $L$ 对 $w,b$ 的偏导数就可以更新参数。

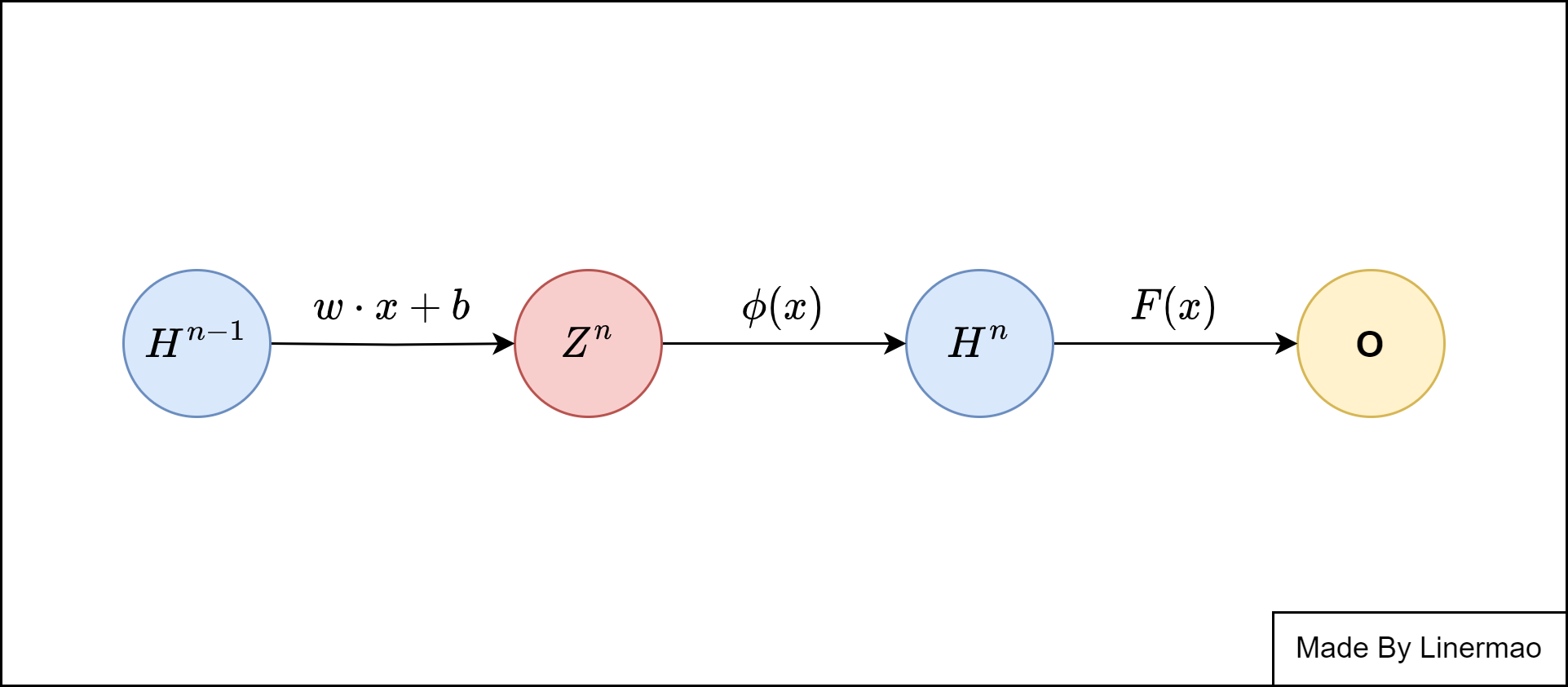
图2-1

我们先来规定几个变量的意义与写法：

$$F(x) = Softmax(x) \ or \ others$$ $$\phi (x) = activate(x)$$ $$\mathbf{w^n} = \begin{bmatrix} w^1_1 & w^2_1 & \dots & w^c_1 \\ w^1_2 & w^2_2 & \dots & w^c_2 \\ : & : & & : \\ w^1_d & w^2_d & \dots & w^c_d \end{bmatrix} , c = lenth \ of Z^{n},d = lenth \ of H^{n-1}$$ $$\mathbf{b^n} = \begin{bmatrix} b_1 \\ b_2 \\ : \\ b_c \end{bmatrix}$$

接下来我们正式开始推导，我们先从输出层和最后一层隐藏层开始推导，根据我们的定义，我们可以得到：

$$\tag{1-5} \frac{\partial L}{\partial \mathbf{o}} = l'(\mathbf{o^n})$$ $$\tag{1-6} \frac{\partial \mathbf{o}}{\partial \mathbf{h^n}} = F'(\mathbf{h^n})$$ $$\tag{1-7} \frac{\partial \mathbf{h^n}}{\partial \mathbf{z^n}} = \phi'(\mathbf{z^n})$$ $$\tag{1-8} \frac{\partial \mathbf{z^n}}{\partial \mathbf{w^n}} = \mathbf{h^{n-1} \cdot ((h^{n-1} \cdot w^{n}) + b^n)}$$ $$\tag{1-9} \frac{\partial \mathbf{z^n}}{\partial \mathbf{b^n}} = 1$$

我们有链式法则：

$$\frac{\partial L}{\partial \mathbf{w^n}} = \frac{\partial L}{\partial \mathbf{o}} \cdot \frac{\partial \mathbf{o}}{\partial \mathbf{h^n}} \cdot \frac{\partial \mathbf{h^n}}{\partial \mathbf{z^n}} \cdot \frac{\partial \mathbf{z^n}}{\partial \mathbf{w^n}}$$

所以得到了：

$$\tag{1-10} \frac{\partial L}{\partial \mathbf{w^n}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot \phi'(\mathbf{z^n}) \cdot \mathbf{h^{n-1}}$$ $$\tag{1-11} \frac{\partial L}{\partial \mathbf{b^n}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot \phi'(\mathbf{z^n})$$

目标函数 $J$ 对于 $b$ 的偏导不变，对于 $w$ 的偏导还需要加上正则项的导数形式，即：

$$\tag{1-12} \frac{ds}{d\mathbf{w^n}} = \lambda \mathbf{w^n}$$

综合以上，我们就得到了目标函数关于权重与偏置的梯度：

$$\tag{1-13} \frac{\partial J}{\partial \mathbf{w^n}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot \phi'(\mathbf{z^n}) \cdot \mathbf{h^{n-1}} + \lambda \mathbf{w^n}$$ $$\tag{1-14} \frac{\partial J}{\partial \mathbf{b^n}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot \phi'(\mathbf{z^n})$$

但是任务还没完成，上面的推导仅仅是 $n$ 取最后一层时的结果，还没有推导出递推项，所以我们可以继续推导：

$$\frac{\partial L}{\partial \mathbf{w^{n-1}}} = \frac{\partial L}{\partial \mathbf{z^n}} \cdot \frac{\partial \mathbf{z^n}}{\partial \mathbf{h^{n-1}}} \cdot \frac{\partial \mathbf{h^{n-1}}}{\partial \mathbf{z^{n-1}}} \cdot \frac{\partial \mathbf{z^{n-1}}}{\partial \mathbf{w^{n-1}}}$$ $$\tag{1-15} \frac{\partial J}{\partial \mathbf{w^{n-1}}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot \phi'(\mathbf{z^n}) \cdot \phi'(\mathbf{z^{n-1}}) \cdot \mathbf{w^n} \cdot \mathbf{h^{n-2}} + \lambda \mathbf{w^{n-1}}$$ $$\tag{1-16} \frac{\partial J}{\partial \mathbf{b^{n-1}}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot \phi'(\mathbf{z^n}) \cdot \phi'(\mathbf{z^{n-1}}) \cdot \mathbf{w^n}$$

整理一下，我们就得到了一个完整的公式：

$$k = n,n-1,...,2,1$$ $$\tag{1-17} \frac{\partial J}{\partial \mathbf{w^k}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^k}) \cdot [\phi'(\mathbf{z^n}) \cdot \phi'(\mathbf{z^{n-1}})\cdot ... \cdot \phi'(\mathbf{z^k})] \cdot [\mathbf{w^n} \cdot \mathbf{w^{n-1}} \cdot ... \cdot \mathbf{w^{k+1}}] \cdot \mathbf{h^k} + \lambda \mathbf{w^k}$$ $$\tag{1-18} \frac{\partial J}{\partial \mathbf{b^k}} = l'(\mathbf{o^n}) \cdot F'(\mathbf{h^n}) \cdot [\phi'(\mathbf{z^n}) \cdot \phi'(\mathbf{z^{n-1}})\cdot ... \cdot \phi'(\mathbf{z^k})] \cdot [\mathbf{w^n} \cdot \mathbf{w^{n-1}} \cdot ... \cdot \mathbf{w^{k+1}}]$$

写的简洁一点就是：

$$\tag{1-19} \frac{\partial J}{\partial \mathbf{w^k}} = \mathbf{h^{k-1}} \cdot \frac{\partial J}{\partial \mathbf{z^k}} + \lambda \mathbf{w^k}$$ $$\tag{1-20} \frac{\partial J}{\partial \mathbf{b^k}} = \frac{\partial J}{\partial \mathbf{z^k}}$$

然后再使用梯度下降的方法就可以实现权重和偏置的更新。