（五）深度学习之模型初始化

初始化方案的选择在神经网络学习中起着举足轻重的作用，它对保持数值稳定性至关重要。

1. 梯度消失和梯度爆炸

梯度消失和梯度爆炸本质上是一样的，都是因为网络层数太深而引发的梯度反向传播中的连乘效应。

1.1 梯度消失

在反向传播的表达式中可以看出，如果每一组的 $\phi(z) \cdot w$ 都非常小，就会导致减去的梯度值非常小，参数基本得不到更新，又因为下一轮又会导致梯度值非常小，就产生了 梯度消失 的问题。

如果激活函数的选择不合适，比如使用 Sigmoid，也容易出现梯度消失现象。

下图为 Sigmoid 函数的导数函数图像：

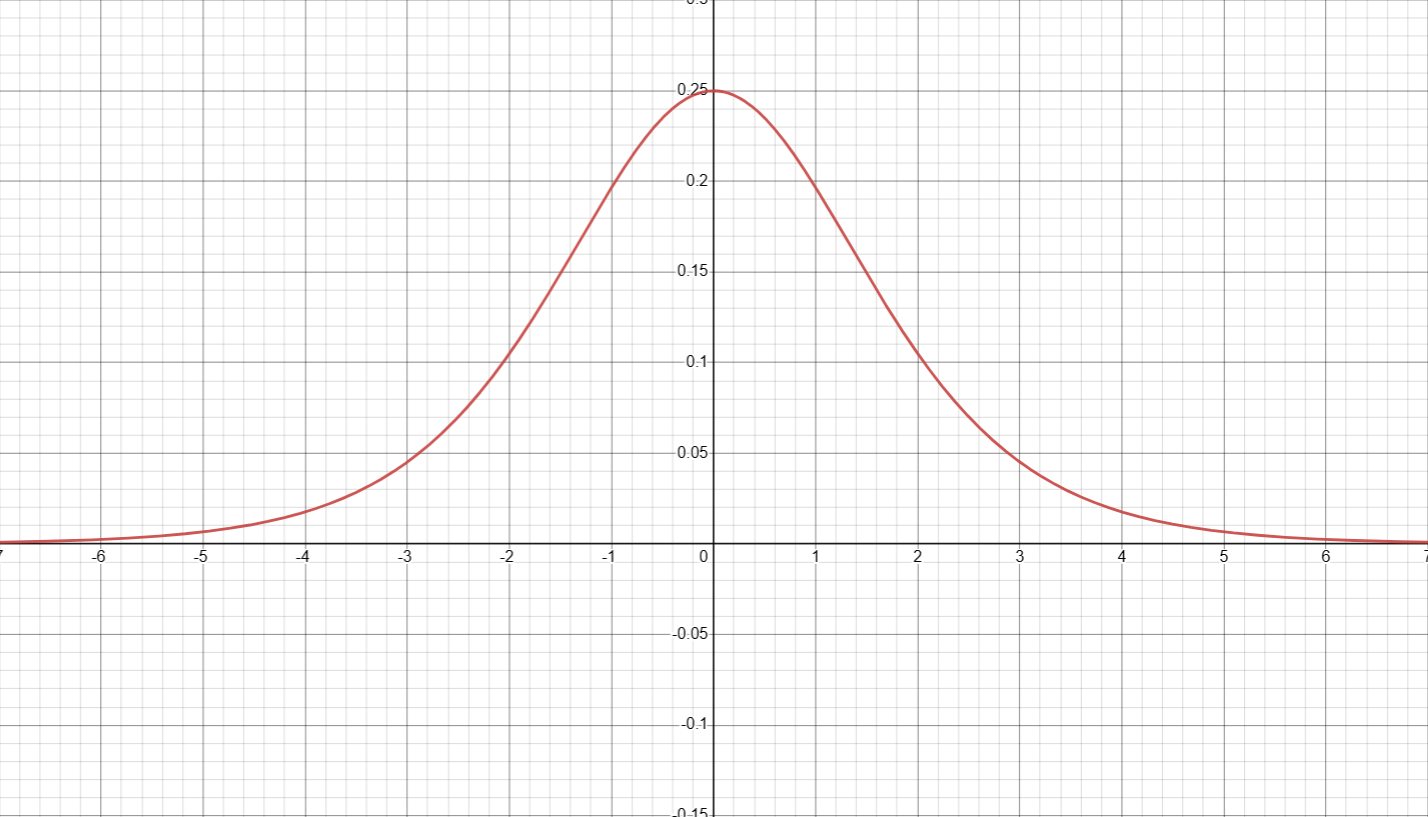
图1-1

我们发现 Sigmoid 函数的导数不超过 $0.25$ ，所以容易产生梯度消失问题。

1.2 梯度爆炸

梯度爆炸 与梯度消失相反，误差梯度在更新过程中如果累计到一个非常大的值，会导致梯度大幅度地更新，进而导致网络不稳定。极端情况下，会导致结果溢出 （NaN，无穷与非数值）。

1.3 梯度爆炸优化方法

1.3.1 更换激活函数

如使用 ReLU、Leaky ReLU 和 ELU 等激活函数，因为这些函数的导数通常比 sigmoid 和 tanh 函数大，有助于避免梯度消失。

1.3.2 梯度剪切

梯度剪切主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，更新梯度时，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内，防止梯度爆炸。

梯度剪切还有按模剪切法，当值超过设定值时：

$$\tag{1-1} w = \frac{b}{||w||} w$$

1.3.3 正则化

解决梯度爆炸的手段是权重正则化（weithts regularization）。通过限制权重的大小，权重正则化可以减小梯度的幅度。当梯度的幅度较小时，梯度更新的参数值也会相应地较小，从而减轻了梯度爆炸的问题。

（正则化的内容见（二）深度学习之线性回归 2.3） 。

1.3.4 残差结构

自从残差网络提出后，几乎所有的深度网络都离不开残差的身影，相比较之前的几层，几十层的深度网络，残差网络可以很轻松的构建几百层而不用担心梯度消失过快的问题。具体的内容将放在残差网络专题介绍。

2. Xavier 初始化

如果我们能够取一个合适的权重和偏置初始值，使得更新过程中尽量少地出现过大或者过小，就能很好的减少梯度问题。

Xavier初始化（Xavier Initialization） 的主要思想是在初始化权重时尽可能保持每个神经元输出方差相等。简单来说，它会随机选择每个权重值，并根据某种特定的分布对其进行缩放，以使分布的方差在反向传播过程中保持不变。实际上，Xavier 初始化隐含了一个假设，那就是前一层输出和该层输入的方差相等。通过这种初始化方式，可以使得每个神经元之间的输出方差尽量一致，防止梯度消失或梯度爆炸问题的发生。因此，使用 Xavier 初始化可以在训练深度神经网络的时候更容易地实现收敛，并提高训练速度和模型性能。

当使用 Xavier 初始化时，我们首先需要确定要初始化的层中神经元的数量 $lenth_1$，以及该层前一层中神经元的数量 $lenth_2$ 。然后，我们可以使用以下公式来计算权重矩阵的标准差 $\sigma$ ：

$$\tag{2-1} \sigma = \sqrt{\frac{2}{lenth_1 + lenth_2}}$$

让 $w$ 的值均匀分布：

$$\tag{2-2} w \sim U [\ -\sqrt{\frac{6}{lenth_1 + lenth_2}} \ ,\sqrt{\frac{6}{lenth_1 + lenth_2}} \ ]$$

（等待水平提升后再深入）