（六）深度学习之卷积神经网络

前言

我们接下来使用的卷积的概念不需要深入学习，只需要有大致的印象即可。

推荐观看视频：

1. 卷积

在数学中，给定两个函数 $f,g:R^d \rightarrow R$ ，我们定义 卷积（Convolution） 为：

$\tag{1-1} f(s)*g(s) = \int_{-\infty}^{\infty} f(x)g(s-x)dx$

在计算机中通常使用离散形式：

$\tag{1-2} f(s)*g(s) = \sum_{-\infty}^{\infty} f(x)g(s-x)dx$

（等待水平提升后再深入）

2. 图像卷积

卷积神经网络的设计主要是是用于研究图像数据，接下来我们研究如何将图片的信息提取出来。

2.1 二维卷积

我们现在有两个矩阵，姑且先称为大矩阵 $A$ 和小矩阵 $B$ 。我们定义 $A*B$ 的运算法则为：从 $A$ 的左上角开始，选取与 $B$ 维数相同的矩阵 $C$ 内的数与 $B$ 对应位置的数进行点乘求和运算。

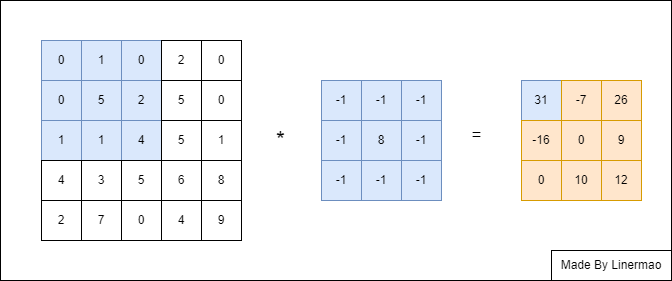
图2-1

$C$ 矩阵也可以叫做 窗口矩阵。

在这里，我们称矩阵 $B$ 为 卷积核（Convolution Kernel）。一般而言，卷积核都是奇数长宽，这样才会拥有中心核。

实际上，我们这里的运算不能称作卷积，而是互相关运算（Cross-Correlation），因为卷积运算还需要我们水平和垂直翻转卷积核。但是由于卷积核是从数据中学习到的，因此无论这些层执行严格的卷积运算还是互相关运算，卷积层的输出都不会受到影响，所以我们可以将这样的互相关运算称作卷积运算，虽然严格意义上他们并不等同。

2.2 填充与步幅

我们在 2.1 中可以发现，卷积的输出形状取决于输入形状和卷积核的形状，也就是说，输出形状为：

$\tag{2-1} [n_h - k_h + 1]\times[n_l - k_l + 1]$

其中，$n_h,n_l,k_h,k_l$ 分别为矩阵的行数和列数。

在应用多层卷积时，我们常常丢失边缘像素。解决这个问题的简单方法即为 填充（padding），在输入图像的边界填充元素（通常填充元素是 $0$）。

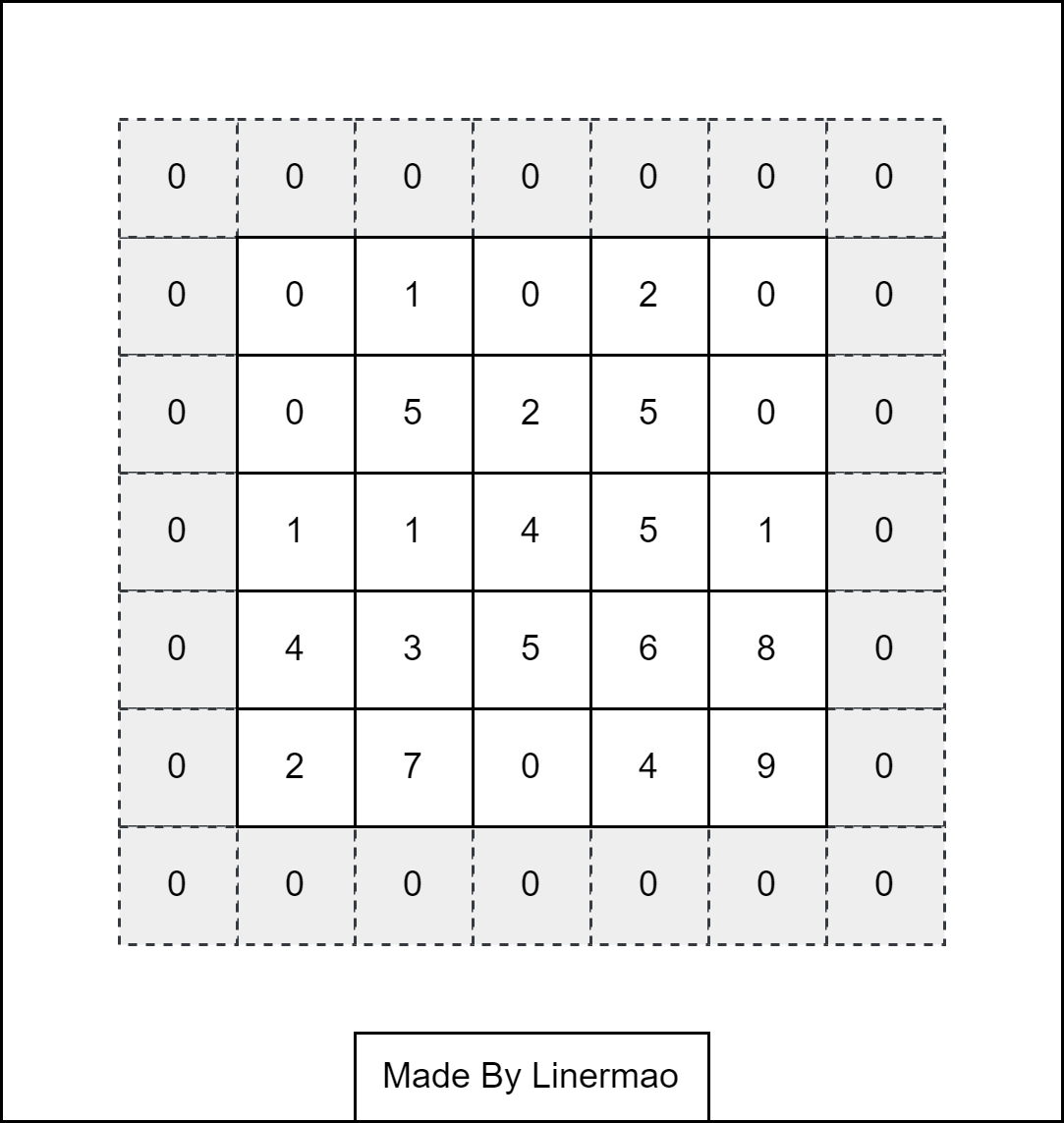
图2-2

我们定义添加的行数为 $p_h$ ，列数为 $p_l$ ，并且让添加的行列数尽量平均分配在两侧。通常，我们让 $p_h = k_h - 1$ ， $p_l = k_l - 1$ 。

所以形状修改为：

$\tag{2-2} [n_h - k_h + p_h + 1]\times[n_l - k_l + p_l + 1]$

我们将每次滑动元素的数量称为 步幅（stride） ，在第一个式子里我们假定了步幅为 $1$ ,也就是说窗口每次滑动一行或一列。我们假设步幅为 $s_h,s_l$ ，更新公式：

$\tag{2-3} [(n_h - k_h + p_h + s_h)/s_h]\times[(n_l - k_l + p_l + s_l)/s_l]$

2.3 三维卷积

输入数据是图像时，图像通常是高、长、通道（channel） 方向上的3维形状，例如彩色图像具有标准的RGB通道来代表红、绿和蓝。所以我们使用三维卷积的方法进行处理：

三维位卷积的方法与二维类似，先按照二维卷积的方法计算出所有通道的值，最后相加。

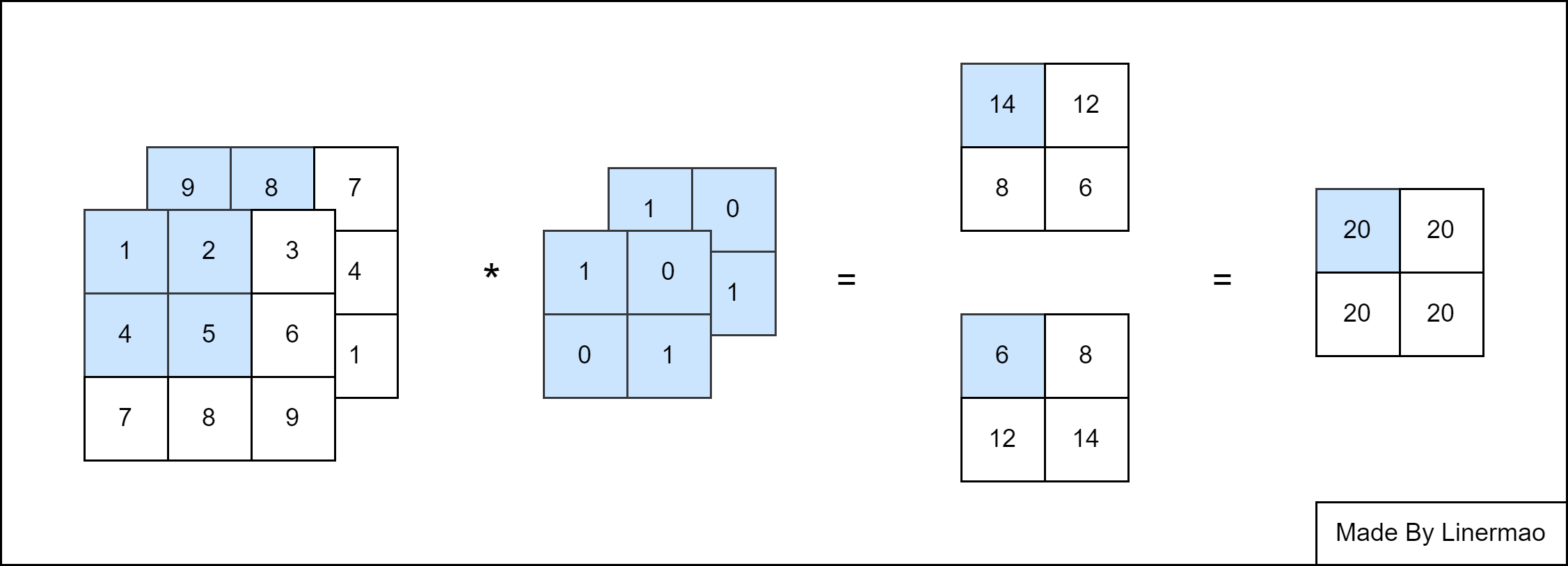
图2-3

这叫做多通道输入（Multi-Channel Input）。

我们现在还只有一个输出通道，我们也可以设置多个卷积核来得到多个通道的输出结果，这叫做多通道输出（Multi-Channel Output）。

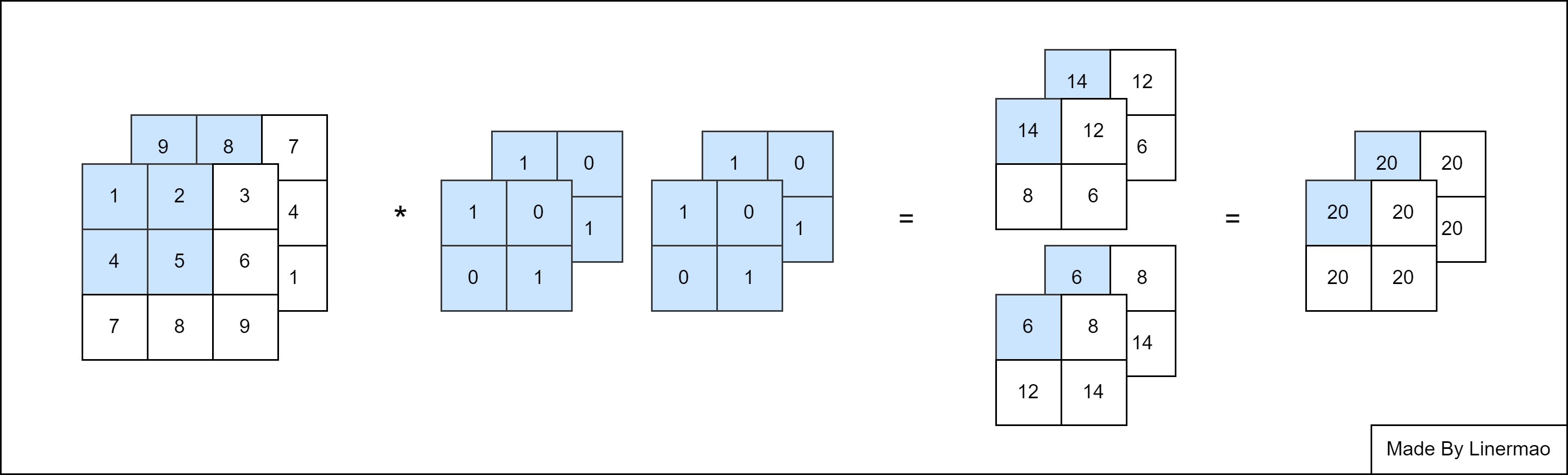
图2-4

3. 卷积神经网络

卷积神经网络（Convolutional Neural Network） 就是依靠三维卷积运算进行的神经网络，可以很有效的减少训练参数，加快训练速度。

卷积神经网络可以很好的提取高维数据组的信息，但是训练的开销很大，一般需要使用 GPU 运算，并且得到的卷积层信息物理含义不明确，也就是得到了一个 “黑箱模型” 。

卷积神经网络的基础架构如图所示：

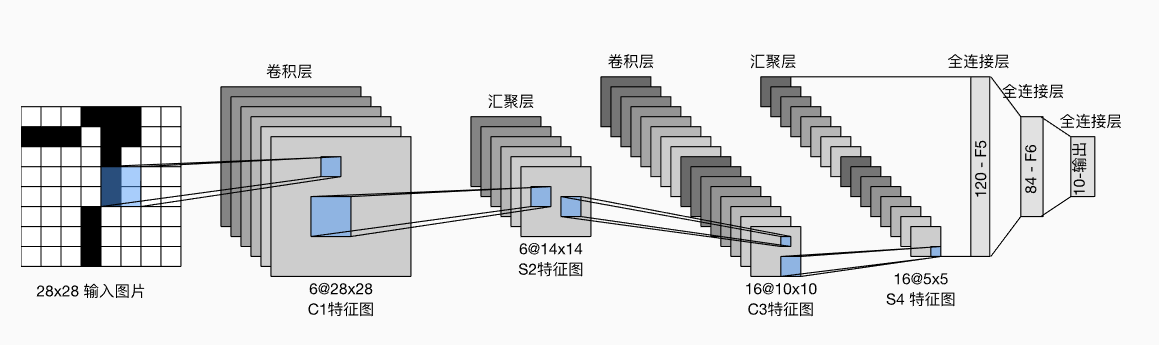
图3-1

图片来自《动手学》

可以简化为：

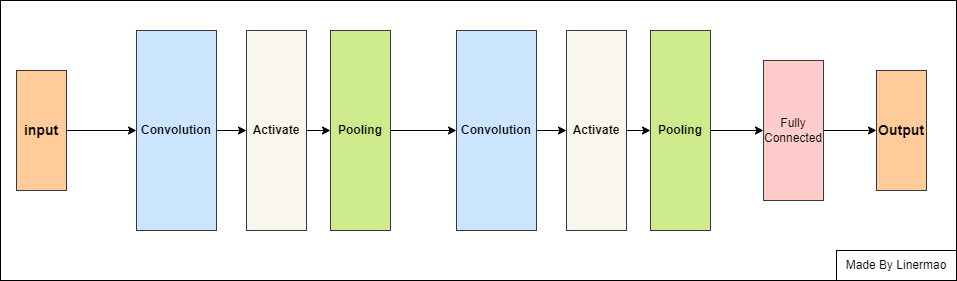
图3-2

相较于人工神经网络，卷积神经网络多了 卷积层 和 池化层 。

3.1 卷积层

卷积层（Convolution Layer） 是构建卷积神经网络的核心层，它产生了网络中大部分的计算量。

卷积层的输入数据称为 输入特征图（input feature map） ，输出数据称为 输出特征图（output feature map） 。

最基本的卷积层就在做下图的事情，中间的运算遵守三维卷积运算：

图3-3

当然，输入输出也可以是更多维数的。

3.2 卷积层计算量

假设有一个三维数据输入，大小为：

$channel_1 \times h \times l$

通过一个核函数，结构为：

$channel_2 \times channel_1 \times k_h \times k_l$

那么会输出大小为

$channel_2 \times r_h \times r_l$

其中：

$r_h \times r_l = [(n_h - k_h + p_h + s_h)/s_h] \times [(n_l - k_l + p_l + s_l)/s_l]$

每一次卷积计算会涉及到 $k_h \times k_l$ 次运算，所以一个卷积层的计算量为：

$\tag{3-1} channel_1 \times channel_2 \times r_h \times r_l \times k_h \times k_l$

3.3 池化层（汇聚层）

池化层（Pooling Layer） 可以用来减少参数。通过对输入的降维，有效减少后续层需要的参数。

当输入中像素在邻域发生微小位移时，池化层的结果不变，这可以增强网络的鲁棒性，有一定抗扰动的作用。

常见的池化层方法有 最大池化（Max Pooling），平均池化（Average Pooling）。

3.3.1 最大池化

最大池化(Max Pooling) 是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。输出矩阵的维数计算方法同二维卷积运算。

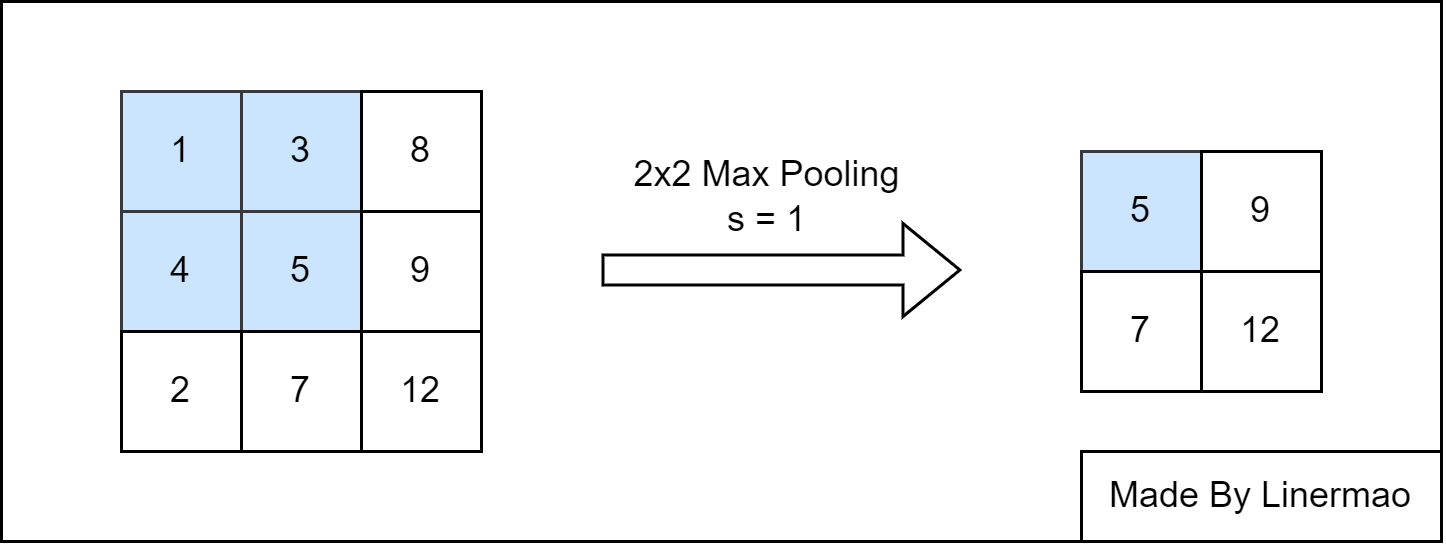
图3-4

3.3.2 平均池化

平均池化(Average Pooling) 是将输入的图像划分为若干个矩形区域，对每个子区域输出所有元素的平均值。

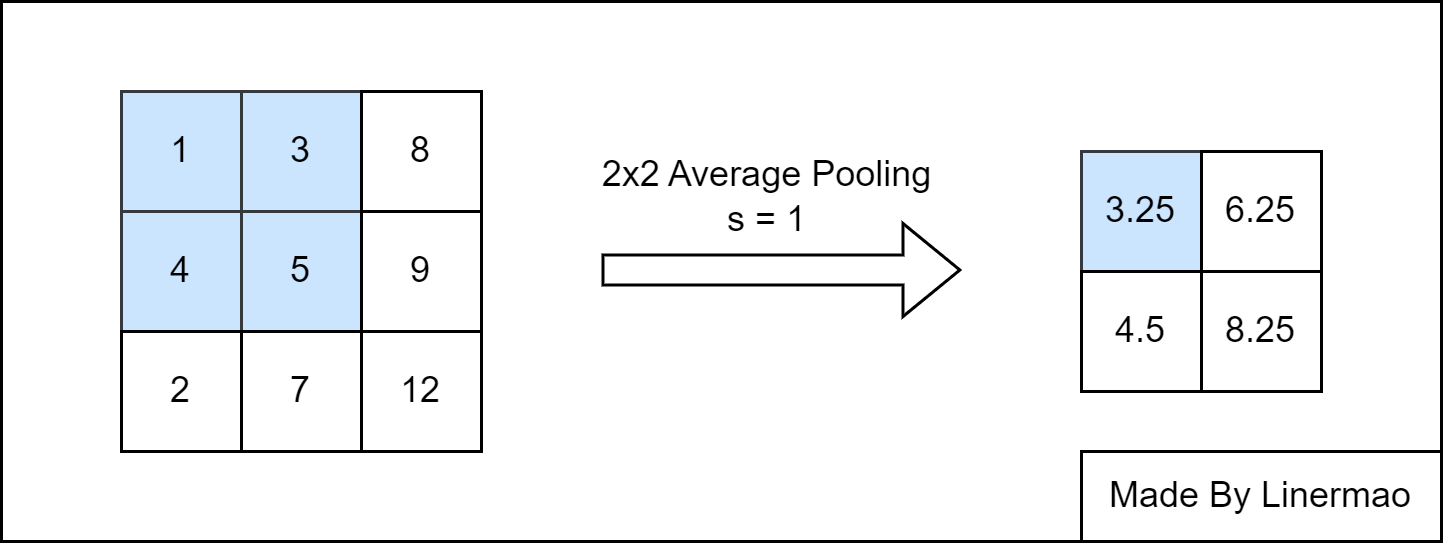
图3-5

3.4 感受野

感受野（Receptive Field），指的是神经网络中神经元 “可见的” 输入区域，在卷积神经网络中，特征图上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。

图3-6

图片来源网络

一般来说感受野越大越好，如图像分类中最后卷积层的感受野要大于输入图像，网络深度越深感受野越大性能越好密集预测要求输出像素的感受野足够的大，确保做出决策时没有忽略重要信息，一般也是越深越好。

感受野计算时一般不考虑池化层的影响，计算公式：

$RF_{l+1} = RF_l + (KernelSize_{l+1}-1) \times \prod_{i=1}^l stride_i$

$RF$ 表示感受野大小， $l$ 表示层数，$KernelSize$ 表示卷积核大小，$stride$ 为步幅大小。

3.5 1x1卷积核

1x1卷积核 也称 网中网（Network in Network） ，指长宽均为 $1$ 的卷积核，因此对于输入特征图主要作用在其通道上，实现 通道信息交流 。

1x1卷积核还有一个重要的作用便是它可以表示卷积层的全连接关系。

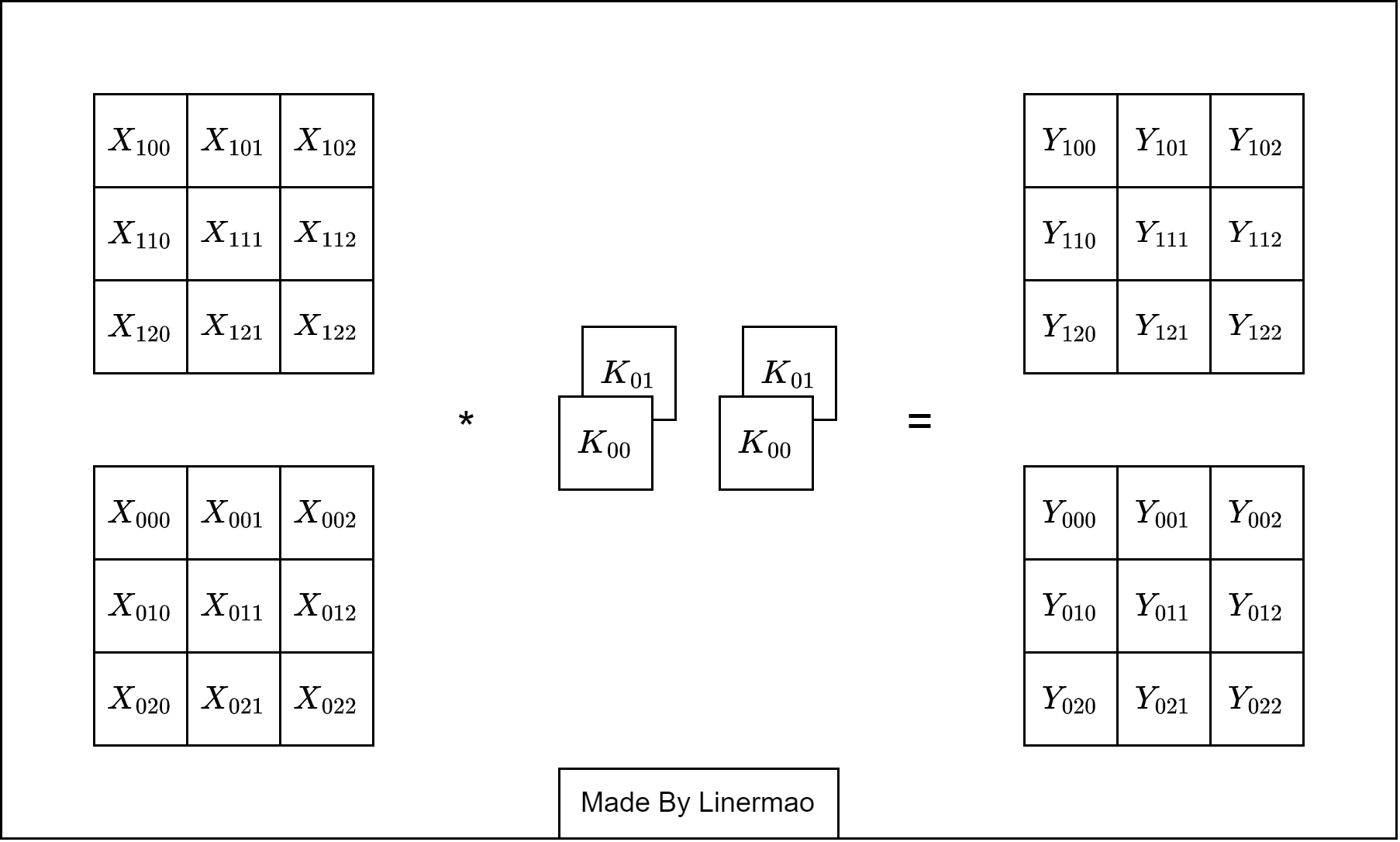
图3-7

不难看出：

$\mathbf{Y_{0}} = K_{00} \cdot \mathbf{X_{0}} + K_{01} \cdot \mathbf{X_{1}}$ $\mathbf{Y_{1}} = K_{10} \cdot \mathbf{X_{0}} + K_{11} \cdot \mathbf{X_{1}}$

我们用全连接层的方式表达这种函数关系：

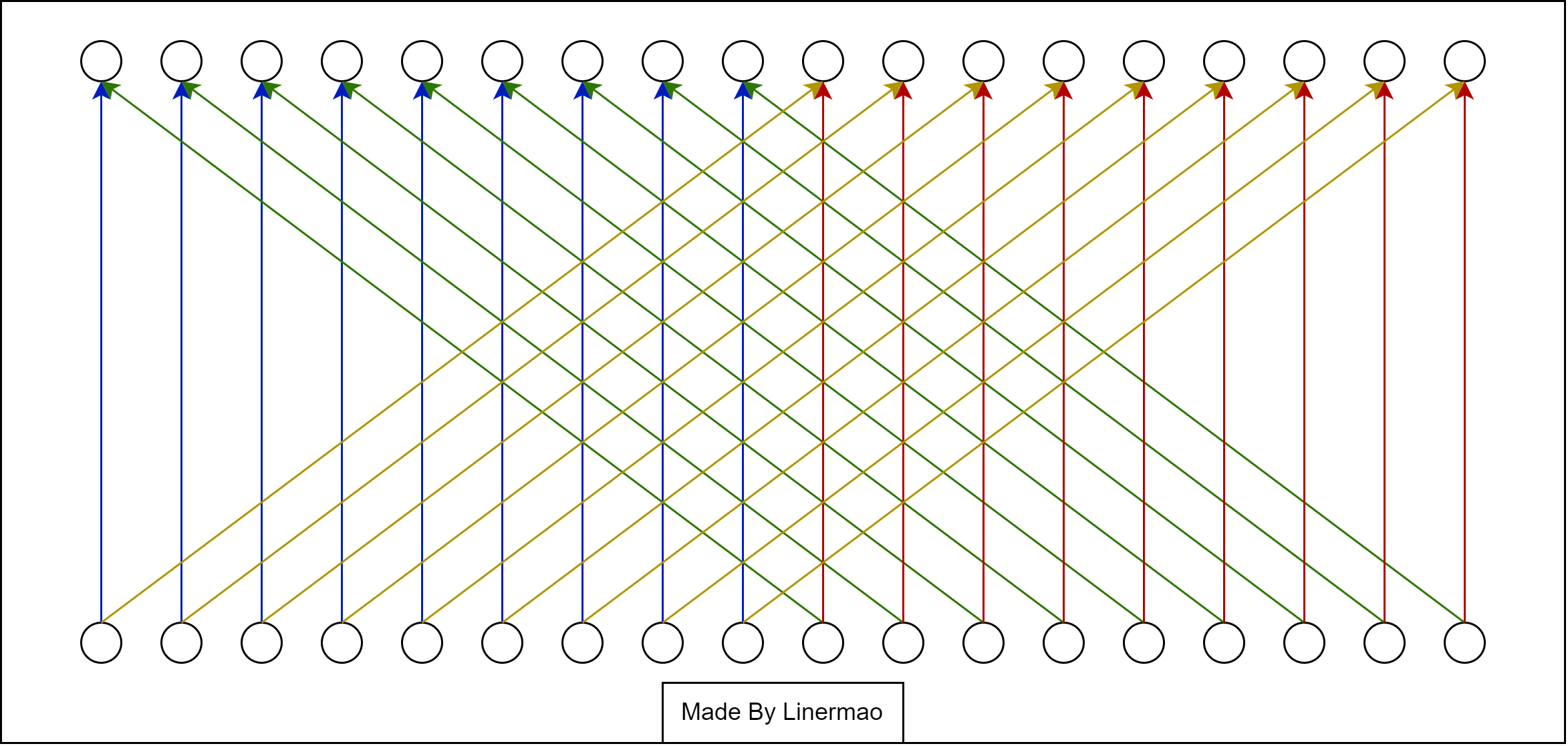
图3-8

可以发现，结构与全连接层非常像，图中所缺失的连线我们就设定其权重为 $0$ 。我们还可以观察到，同一颜色的连线对应的权重值是一致的。

所以 1x1卷积核可以用来将卷积层转化为全连接层计算。