（八）深度学习之残差网络

1. 残差网络的由来

2012 年， AlexNet （深度卷积神经网络）取得了 ILSVRC 挑战赛的冠军，并且大幅领先第二名，由此引发对深度网络的广泛研究，树立了一个信念 —— “越深的网络准确率越高” 。

通过实验，随着网络层不断的加深，模型的准确率先是不断的提高，达到最大值，然后随着网络深度的继续增加，模型准确率毫无征兆的出现大幅度的降低。

这个现象与“越深的网络准确率越高”的信念显然是矛盾的、冲突的。ResNet 团队将这一现象称为 退化（Degradation）。

ResNet 团队认为退化出现的原因是深度网络在非线性转化中走得太远，数据被映射分散到更加离散的空间，使得网络难以实现简单的线性变化。

为了解决这样的问题，ResNet 团队引入了一个具有 快捷链接（Shortcut Connection） 的结构 —— 残差块，并且使用残差块的基础上构建了残差网络。

残差（Residuals） 是指实际观测值与回归模型预测值之间的差异。

我们定义网络输入是 $x$ ，网络的输出是 $F(x)$ ，网络要拟合的目标是 $H(x)$ 。

传统网络的训练目标是：

$\tag{2-2} F(x) = H(x)$

残差结构在原先的映射中将输入短接到输出上，使得整个映射变成：

$\tag{2-1} F(x) + x = H(x)$

此时，$F(x) = H(x) - x$ 就体现了残差这一概念。

如果一个深层网络多余的层全部做恒等映射 $F(x) = x$ ，那么浅层网络的解空间理论上应该只是深层网络的一个子集，但是我们观察到了退化现象，所以我们猜测 —— 深度网络已经难以学习恒等映射。

当我们使用 $F(x) + x$ 时，网络只需要学习 $F(x) = 0$ 的映射，相对来说更加简单。这种改进后，深层网络不仅能做到不差于浅层网络，还能超出不少。

而为什么学习 $F(x) = 0$ 的映射会更简单时，本人也还没有透彻理解，按下不表。

残差网络 是由一系列 残差块（Residual Block） 组成的，一个残差块可以表示为下图：

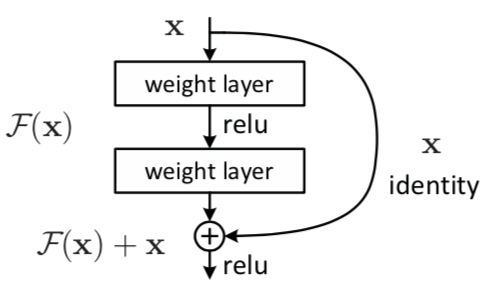
图3-1

图片来自 Deep Residual Learning for Image Recognition

如果 Shortcut 在同维度映射，也就是通道数一致的情况下：

$\tag{3-1} y = F(x,w) + x$

若在不同维度，则需要先对 $x$ 进行线性映射来匹配维度，也就是使用 $1\times1$ 卷积核调整维度：

$\tag{3-2} y = F(x,w) + W_s x$

残差网络就是多个残差块组成的网络结构。

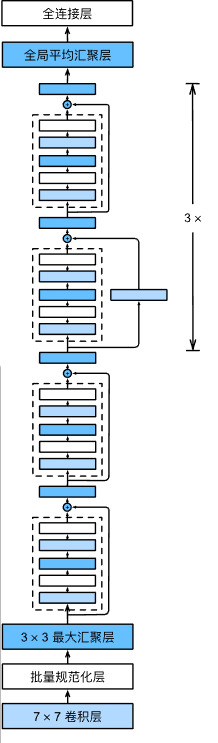
图4-1

图片来自《动手学》

我们可以单独拿出一个残差块来分析：

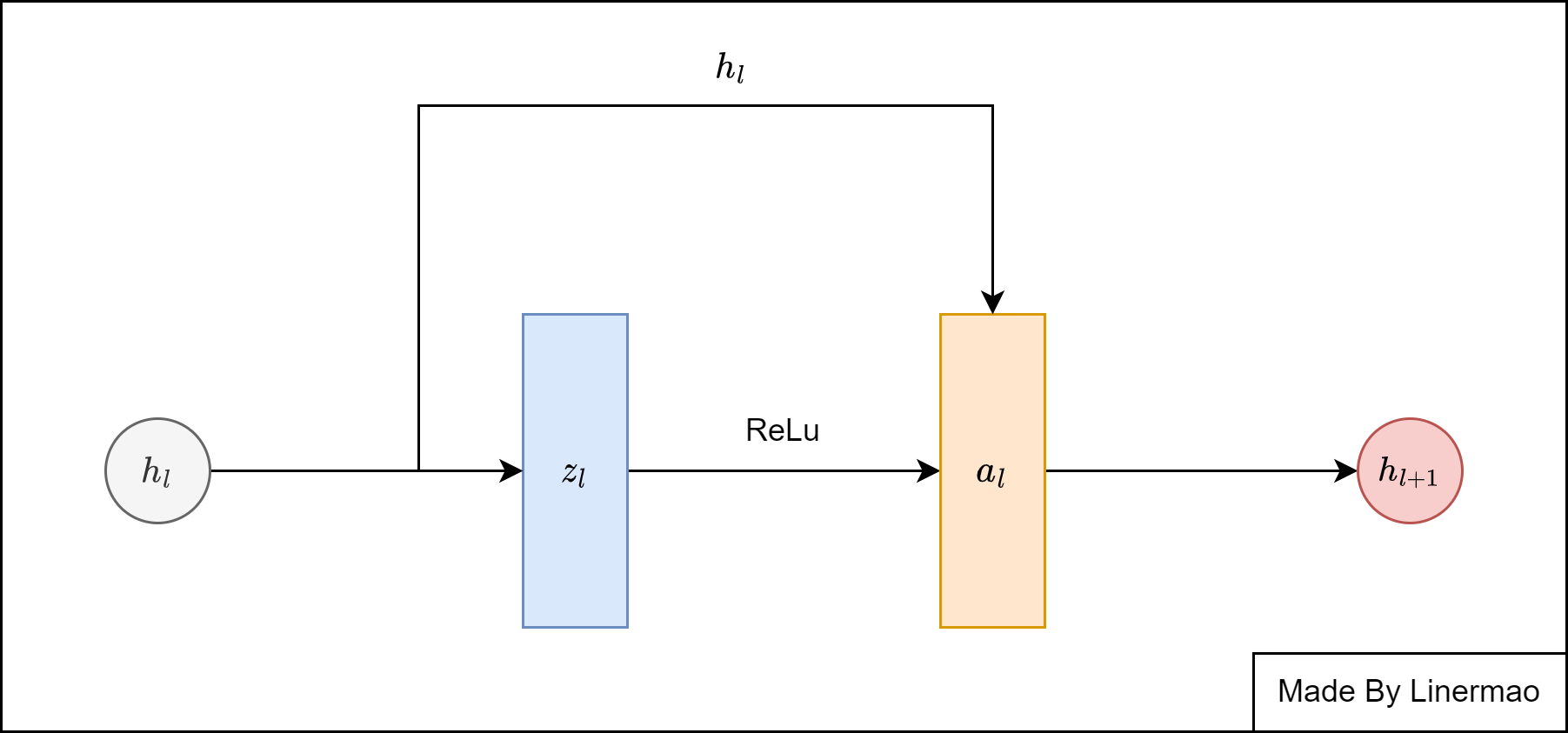
图4-2

我们可以对（3-1）式进行进一步的解释：

$\tag{4-1} h_{l+1} = \sigma(z_{l+1}+h_l)$

进一步拆解：

$\tag{4-2} h_{l+1} = \sigma(w_l\cdot h_l + b_l +h_l)$

在这个式子中，就算出现了梯度消失的问题，下一层会直接训练上一层的值，而不是输出零导致网络结构无法更新。

这样就使得深度网络可以对抗梯度消失的问题，从而加深网络层数，达到更好的训练效果。