(十)深度学习之长短期记忆网络
(十)深度学习之长短期记忆网络
长短期记忆网络
长短期记忆(Long short-term memory, LSTM) 是一种特殊的 RNN ,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的 RNN,LSTM 在更长的序列中能够有更好的训练表现。
LSTM 的基本模型如图所示:
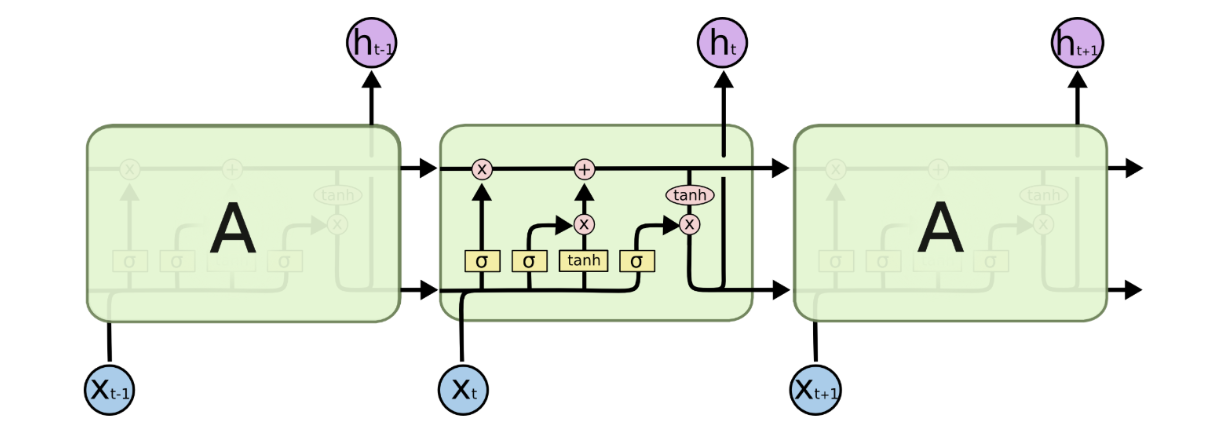

图1-1
这张图也许太过于专业,晦涩难懂,我们可以按照 RNN 的结构将 LSTM 表示出来:
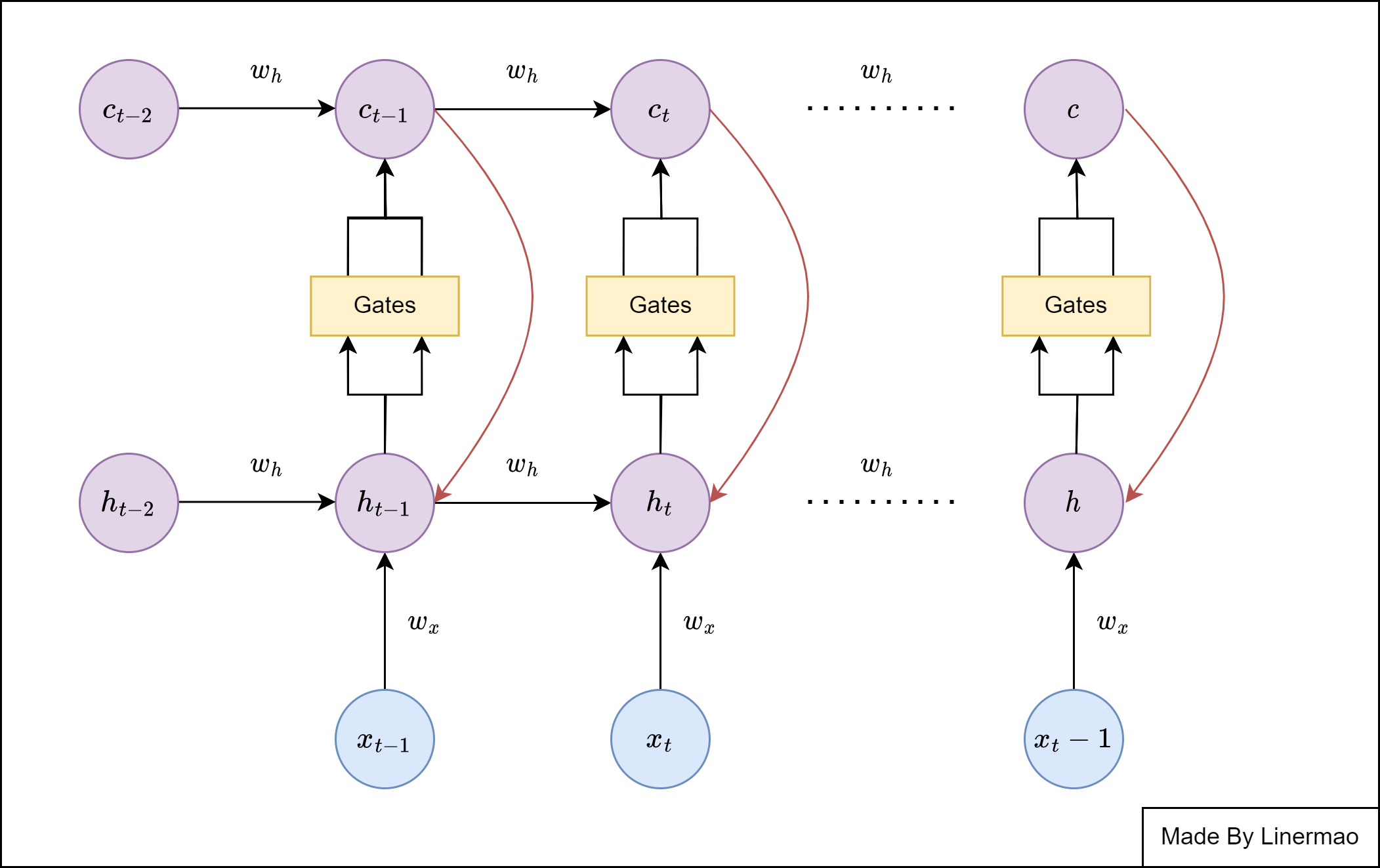
图1-2
相较于 RNN 结构,LSTM 添加了 “门” 结构,在最上层也多了一条路线。
我们可以简单的理解为这样:
每次我们在进行记忆时,还将我们的记忆写在 “笔记本” 上,也就是 记忆细胞 上,而笔记本也是我们每次记忆时需要参考的内容。门结构主要进行笔记本的增添与删减两件事。每次记忆结束时,我们的记忆还会受到笔记本内容的影响,而笔记本相对来说不容易丢失,所以可以记忆更长期的内容。
接下来我们将 LSTM 结构分成四个部分详细介绍。
遗忘门
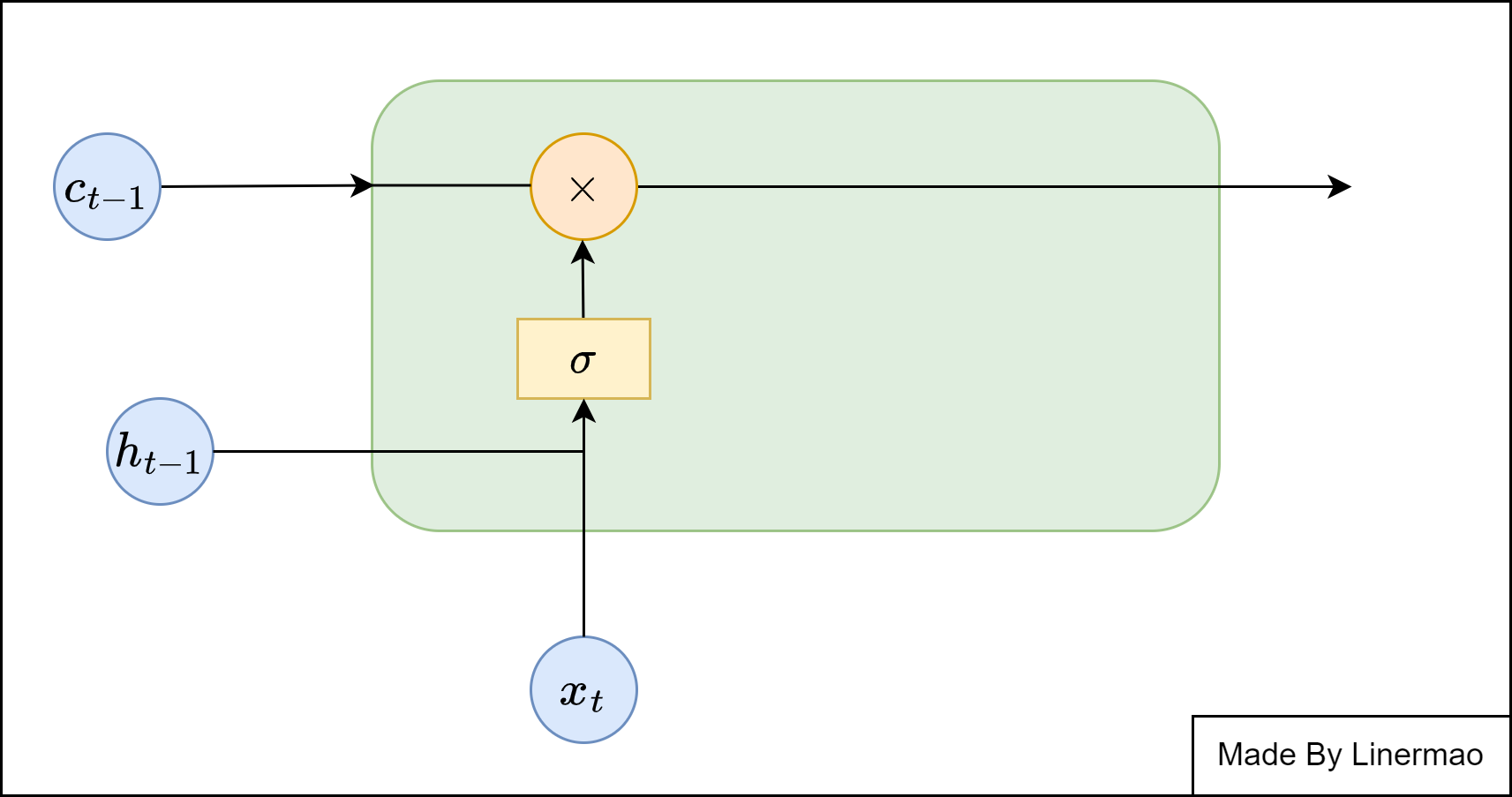
图1-3
对于上一时刻 LSTM 中的单元状态来说,一些信息可能会随着时间的流逝而 “失效”。为了不让过多记忆影响神经网络对现在输入的处理,我们应该选择性遗忘一些在之前单元状态中的分量——这个工作就交给了 “遗忘门”
给出数学公式:
我们选取 $\sigma$ 激活函数为 Sigmoid 激活函数,由于 Sigmoid 的特性,会将值压缩到 $[0,1]$ 的区间内,而且大部分十分接近 $0 \ or \ 1$ ,所以我们让记忆细胞与得到的输出向量相乘就可以选择性遗忘无用的信息。
公式如下:
输入门
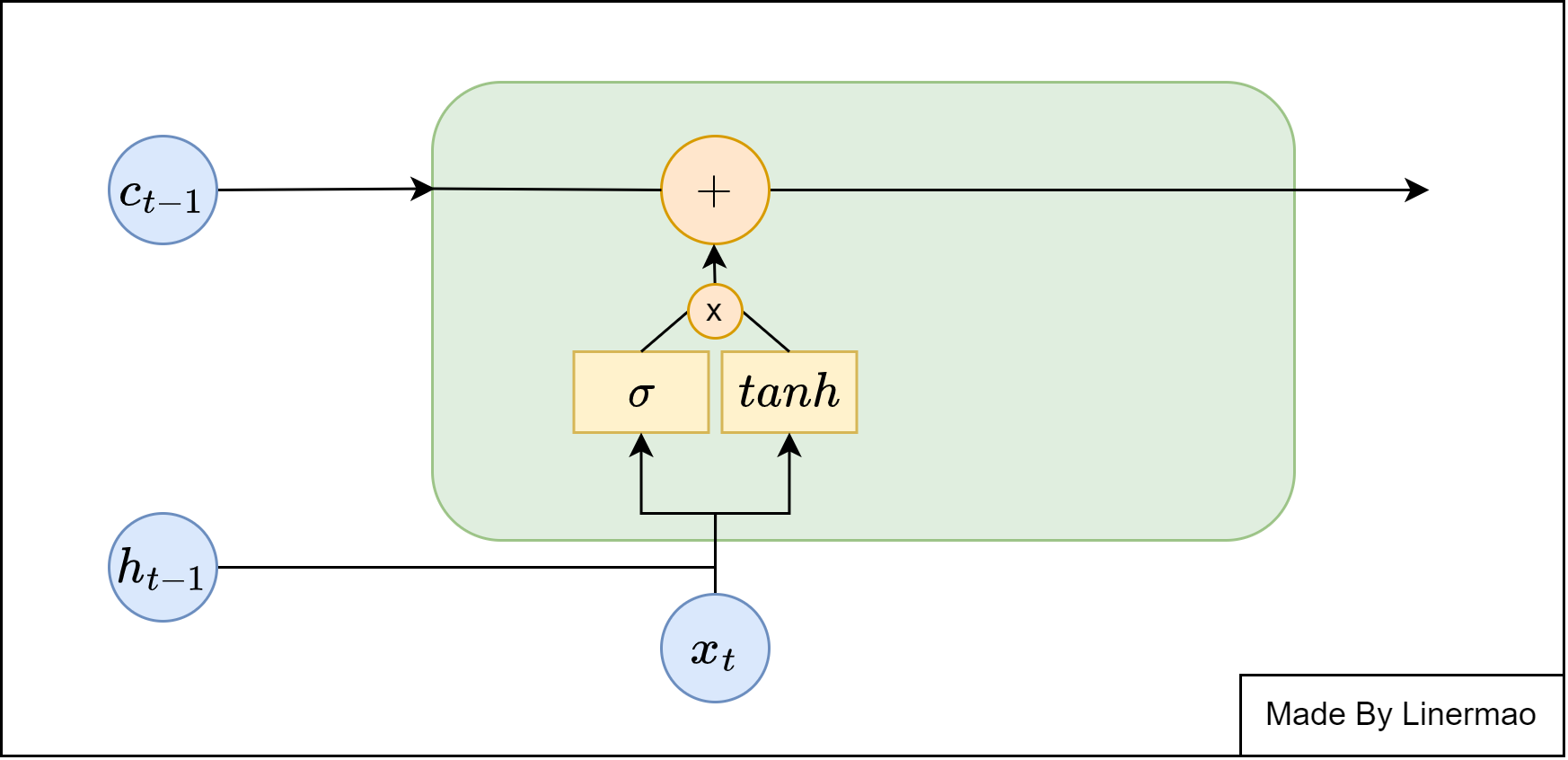
图1-4
输入门是用来控制是否将此时刻的数据写入记忆细胞。
给出数学公式:
我们使用 $tanh$ 作为激活函数,将数据压缩到 $[-1,1]$ 的范围内,可以看作是一种提取有效信息的手段,然后使用 $Sigmoid$ 激活函数,将得到的结果进行向量相乘,进行记忆数据的筛选,然后写入记忆细胞。
公式如下:
至此,我们也完成了记忆细胞的前向传播:
输出门
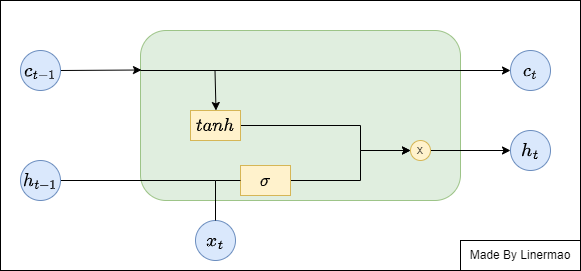
图1-5
LSTM 计算当前时刻的输出值时,输出层会先根据记忆细胞内拥有的信息来调整最后的输出。
给出数学公式:
整合一下现阶段得到的所有公式:
